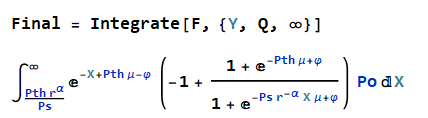Given an Exponentially Distributed Random Variable $X\sim \exp(1)$. I need to find E[P_v] in Mathematica, where $P_v$ is given as:
$$ P_v= \left\{ \begin{array}{ll} a\left(\frac{b}{1+\exp\left(-\bar \mu\frac{P_s X}{r^\alpha}+\varphi\right)}-1\right), & \text{if}\ \frac{P_s X}{r^\alpha}\geq P_a,\\ 0, & \text{otherwise}. \end{array} \right. $$
My Take:
First, let's solve the equation for $P_v$. For that, let's assume g(x) to be:
$$g(x) = \frac{P^0}{\exp(\overline{\mu}P_{th} + \varphi)}\left( \frac{1+\exp(-\overline{\mu}P_{th} + \varphi)}{1 + \exp(-\overline{\mu}P_s x r^{-\alpha} + \varphi)} - 1\right),$$
Then,
$$ P_v = \begin{cases} g(x) & x \geq \frac{P{th}}{Ps}r^\alpha\ 0 & x < \frac{P{th}}{Ps}r^\alpha \end{cases} $$
Then, with the knowledge that the PDF for Exponentially distributed RV is $f(x) = e^{-\lambda x}$ (with $\lambda = 1$ for our case), we can find $\mathbb{E}[P_v]$. (I am not sure if the following is correct or not).
$$ \mathbb{E}[P_v]= \int_Q^\infty g(x)f(x)dx \ \ \ \ \ \ \ \ \ \ \ (1) $$ where $Q = \frac{P_{th} r^{\alpha}}{P_s}$. Now, I solved Eq. (1) in Mathematica but did not get the solution. The Figure below shows my try in Mathematica.
F1 = Po/E^(-\[Mu] Pth + \[CurlyPhi])*((+ E^(-\[Mu] Pth + \[CurlyPhi]))/(+ E^(-\[Mu] Ps X r^(-\Alpha]) \[CurlyPhi])) - 1);
F2 = E^(-X);
F = F1*F2;
Q = (Pth r^\[Alpha])/Ps;
Final = Integrate[F, {Y, Q, \[Infinity]}]