Here is a solution. I've picked a function that I am fond of, but you can adapt to your own purposes:
function which takes the name of function of one argument, a position to evaluate the derivative and a parameter that will be used for the tangent.
tangentLine[func_, loc_, param_] :=
Module[
{deriv, x},
deriv = D[func[x], x] /. x -> loc;
deriv (param - loc) + func[loc]
]
For example:
f[t_] := t^2 + Cos[t]
tangentLine[f, 2, z]
Here it is with a function that I have defined within a module, others might have put the function definition in an Initialization, but I think this is easier to read.
Module[
{
myFunction,
tangent,
t
},
myFunction[0] = 0;
myFunction[1] = 0;
myFunction[x_] := 3 x (1 - x) + (x Log[x] + (1 - x) Log[1 - x]);
Manipulate[
tangent = tangentLine[myFunction, where, t];
Plot[myFunction[z], {z, 0, 1},
Epilog -> {Red,
Line[{{0, tangent /. t -> 0}, {1, tangent /. t -> 1}}]}
],
{{where, 0.25}, 0, 1}
]
]
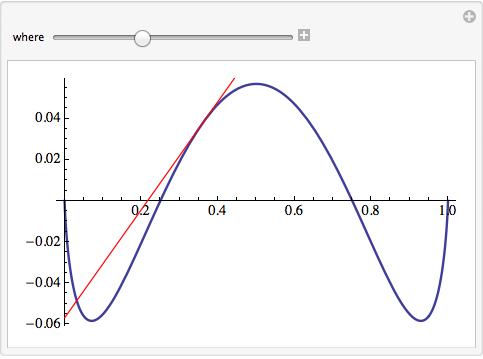
Example result: