Graph transformation models have been around ever since the 60s and there have been many competing paradigms such as: algebraic graph transformation, hyperedge replacement, node label controlled rewriting, algorithmic graph rewriting and so on.

In my opinion the Wolfram Model incorporates some elements from all of these, but most importantly I'd like to draw a parallel with the algebraic one. In the algebraic approach the rules are given by graph morphisms and the pushout can be seen as the realization of the rule.

To make matters concrete, consider the example below from:

https://steemit.com/mathematics/@markgritter/pushouts-on-graphs

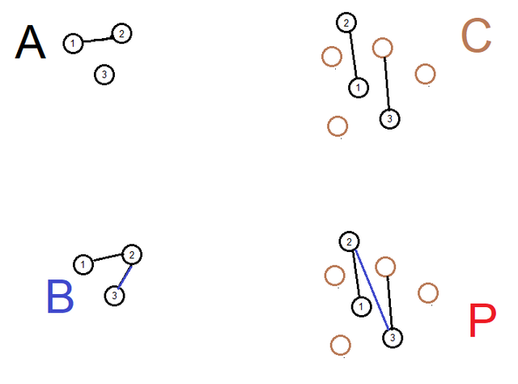
As he puts it, we can think of the graph morphism A->B as a "rule" for changing A, and the morphism A->C as "the location of A in the graph C", the pushout then produces the adequate changes between nodes in the graph by placing the edges in the correct place.

However, in the Wolfram model we're mostly interested in the emerging behavior after the iteration of the rule, something that I don't find discussed very often on these models. It isn't unlikely though that the Wolfram Model could be thought of as sort of an extension of existing models, iteration being a key aspect, in what one might call a n-pushout approach consisting of sequential pushouts.

If such a connection truly exists the applications could be undoubtedly interesting. My interests in the results of graph rewriting theory lie in the possibility to classify the universes so far discovered in terms of systems of categories as is done in the algebraic approach as well as to explore consequences to the Wolfram Model of the concurrency and parallelism theorems present in this approach. Exploring connections with other graph transformation models also opens the doors to consider more general context sensitive grammar rules. I'm aware that Stephen is reluctant to consider rules that aren't exactly fixed, but it seems only natural to me to consider this more general case and also have rules that are dependent of context in the model since their dynamics could very much so translate interesting physical phenomena.

I'm currently following the book Fundamentals of Algebraic Graph Transformation by H. Ehrig and others as well as the Handbook of Graph Grammars and Computing by Graph Transformation edited by G. Rozenberg to try to better formulate my ideas of a possible connection with the Wolfram model. It would be great to see more collaboration between Stephen and people from this field.