I am trying to solve the integral resulting from a convolution between a stretched single exponential decay and a gaussian function.
In the simpler case using just a single exponential decay function:
F[t] = exp^(-t/τ)
and a Gaussian function:
R[t] = 1/(σ*Sqrt(2*π)*exp^(-t^2/(2*σ^2))
I obtain the convolution integral:
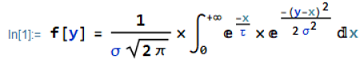
with Mathematica the solution of this integral is:
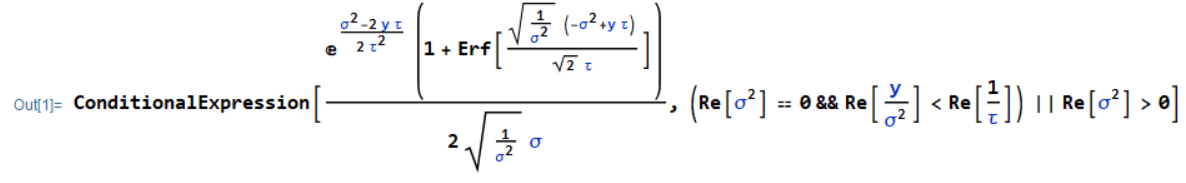
which I know is the correct result.
Now, if I try to change a bit the exp function importing the beta parameter and therefore make it a streched exponential,
F[t] = exp^[(-t/τ)^b] , 0<=b<=1
the convolution integral is:
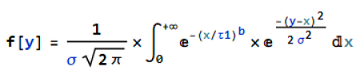
for this integral I do not get a solution
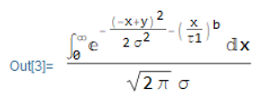
but, the same expression. Is it a matter of defining the parameters? e.g. 0<=b<=1 I am new in Wolfram, thus I couldn't get over this issue and any help will be appreciated.