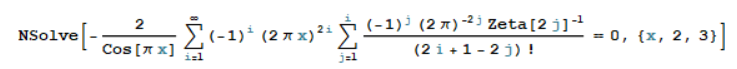Group Abstract Group Abstract

Message Boards Message Boards

Using NSolve to solve equation given by power series?

Anonymous User
Anonymous User
Posted 4 years ago

I have no idea how to numerically solve a transcendental equation given by a power series. Being a power series, I don't know if I need to use infinity or some number of partial terms in the series. It seems Mathematica sucks for this type of equation, since everything I've tried so far failed miserably. I found FindMinimum could be an option, but then the stupid formula doesn't allow an interval, it's always like that (actually, it complains about MachinePrecision).

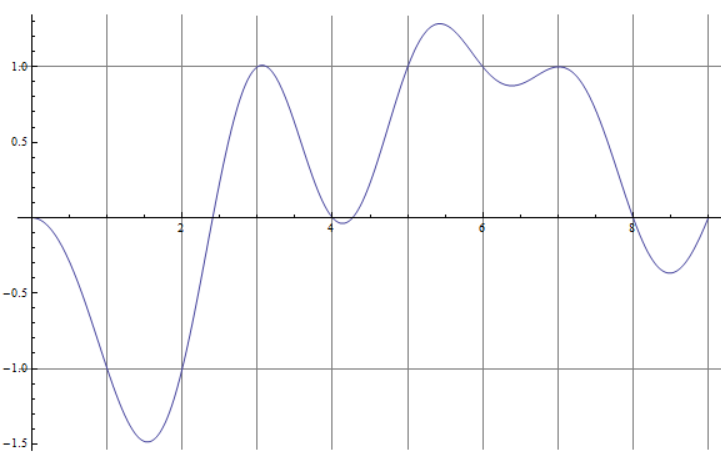
When I plot a graph, ListPlot works using $N=16*x$ terms for each $x$ (see attached graph), but then it's really difficult to get the real values for which $f(x)$ is 0.

I'm only interested in real roots, and if $f(x_0)<=10^{-30}$, $x_0$ is good enough. Here's the equation in input form (I know the syntax here is wrong, I was trying to use a range that I know contains a zero from the plot, one is between 2 and 3, for example -- see graph):

NSolve[(-(2/Cos[Pi*x]))*Sum[(-1)^i*(2*Pi*x)^(2*i)*

     Sum[(-1)^j/((2*Pi)^(2*j)*Zeta[2*j]*(2*i + 1 - 2*j)!), {j, 1, 
       i}], {i, 1, Infinity}] == 
     0, {x, 2, 3}]

Does anybody know this? Thanks

PS - the division by cosine is just removing all the half-integers as roots (other roots are the square-full integers). This is nothing but the Mobius $\mu(x)$ function without those roots.

enter image description here enter image description here
POSTED BY: Anonymous User
8 Replies
Sort By:

I attached my best guess. I hope it helps.
POSTED BY: John Baxter
Anonymous User
Anonymous User
Posted 4 years ago

Thanks, but that's too complicated. You can try a simpler version, try to find a real root between 2 and 3, that should be good enough to start with.

Also, not sure if you will understand this, but the power series can be simplified (pls get rid of $\frac{1}{\cos{\pi x}}$ in the series and also replace both $2\pi$ with $\pi$). The new series thus changed will be equivalent to the former one. Then pls try again.
POSTED BY: Anonymous User
Anonymous User
Anonymous User
Posted 4 years ago

Disappointed with Mathematica for this type of problem. I tried all I could've tried to no avail, Mathematica doesn't provide any reasonable solution using NSolve, not even an approximate solution, it's always empty $\rightarrow$ {}. Mathematica let me down.

Here's a link for the article where I wanted to use that: Graph with mysterious roots
POSTED BY: Anonymous User

Hello Jose,

I find the same things as Bill. I copied/pasted your code and tried to get your plot, but that was not successful. There is something wrong somewhere.

I changed your code a bit, and as Bill said, there seems to be a pole in the region of x = 2.5

cc = Table[
  Sum[(-1)^j/((2*Pi)^(2*j)*Zeta[2*j]*(2*i + 1 - 2*j)! // N), {j, 1, i}],  {i, 1, 20}]

ff1[x_, n_] := (-(2/Cos[Pi*x]))* Sum[(-1)^i*(2*Pi*x)^(2*i)*cc[[i]], {i, 1, n}]

Plot[ff1[x, 15], {x, 0, 5}, PlotRange -> {-10, 10}]

And of course, in your code occurs 2/ Cos[Pi*x], which gives rise to many poles. For example

Cos[Pi x] /. x -> 5/2
POSTED BY: Hans Dolhaine
Anonymous User
Anonymous User
Posted 4 years ago

you guys are making the same mistake as me when I first started, it would explode out to infinity leaving me puzzled. It's not gonna work the traditional way, you have to use ListPlot.

Here's the code for you to try:

 $MaxExtraPrecision = 1000; m = 9; k = 100*m; Clear[f, g]; 
f[z_] := N[-(2/Cos[\[Pi] z]) \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(i = 1\), \(Max[16  z, 12]\)]\(
\*SuperscriptBox[\((\(-1\))\), \(i\)] 
\*SuperscriptBox[\((2  \[Pi]\ z)\), \(2  i\)] \(
\*UnderoverscriptBox[\(\[Sum]\), \(j = 1\), \(i\)]
\*FractionBox[\(
\*SuperscriptBox[\((\(-1\))\), \(j\)] 
\*SuperscriptBox[\((2  \[Pi])\), \(\(-2\) j\)] 
\*SuperscriptBox[\(Zeta[2  j]\), \(-1\)]\), \(\((2  i + 1 - 
          2  j)\)!\)]\)\)\), 20]; \[Mu] = 
 Table[{n = m (q - 1)/(k - 1), f[n]}, {q, 1, k}]; g2 = 
 ListPlot[{\[Mu]}, Joined -> True, ImageSize -> Large, 
  PlotStyle -> {Thickness[Tiny]}, 
  GridLines -> {Table[i, {i, 1, m}], Table[f[i], {i, 1, m}]}]

enter image description here
POSTED BY: Anonymous User
Bill Nelson
Bill Nelson
Posted 4 years ago

If I have a challenging root to find then the first thing I do is look at a plot.

I take your expression and rather than summing over i from 1 to infinity, I try summing over i from 1 to 1 or from 1 to 4 or from 1 to 10 or from 1 to 20 and I plot those partial sums. I expect higher terms to get smaller and smaller and the result to quickly look like the large plot you show in your post. And I expect the root in my plot to get closer and closer to the root in your plot. Then I will be able to say that a sum with 4 terms or 20 terms looks like it will be sufficient for what you want to do.

But, if I haven't made a mistake, when I plot any of those partial sums I find a sum that goes to infinity on one side of 2.5 and to -infinity on the other side of 2.5 and there is no root anywhere near 2.5 and the plot looks absolutely nothing like the plot you show in your post.

Is the plot you show really the plot of this function? Can you reproduce what I tried and explain what I am seeing?
POSTED BY: Bill Nelson
Anonymous User
Anonymous User
Posted 4 years ago

Of course.

As I said before, as a rule of thumb I believe setting $M$ to $16 x_0$ gives a very accurate convergence for all $x$ such that $|x|\le x_0$. So for example, $M=50$ is good for $x$ up to 3, but to save on processing time I set $M=16x$ (Mathematica truncates that to an integer value on a sum). And for $|x|<1$, I make $M=12$.
POSTED BY: Anonymous User

Check the documentation on NSolve syntax. That {x,2,3} is useful for FindRoot but not for NSolve.
POSTED BY: Daniel Lichtblau
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard