Celtic Patterns are so beautiful:

CelticBraid[b_, h_] := 
 With[{q = {{White, Rectangle[{0, 0}, {1, 1}], LightCyan, 
      Polygon[{{1/2, 1/4}, {1, 3/4}, {1, 1/4}, {3/4, 0}}], 
      Polygon[{{1/4, 0}, {1/2, 1/4}, {3/4, 0}}], 
      Annulus[{2/4 + 1/8, 1/4 + 1/8}, {Sqrt[2] (1/8), 
        Sqrt[2] (1/4 + 1/8)}, {45 \[Degree], 
        45 \[Degree] + 180 \[Degree]}]}, 
     Black, {Line[{{1/2, 1/4}, {1, 3/4}}], Line[{{3/4, 0}, {1, 1/4}}],
       Line[{{3/4, 0}, {1/2, 1/4}}], 
      Circle[{2/4 + 1/8, 1/4 + 1/8}, 
       Sqrt[2] (1/4 + 1/8), {45 \[Degree], 
        45 \[Degree] + 180 \[Degree]}], 
      Circle[{2/4 + 1/8, 1/4 + 1/8}, 
       Sqrt[2] (1/8), {45 \[Degree], 45 \[Degree] + 180 \[Degree]}]}},
    w = {White, Rectangle[{0, 0}, {1, 1}], LightCyan, 
     Annulus[{1/2, 1/4}, {Sqrt[2] 1/4, Sqrt[2] 1/2}, {Pi/4, 3/4 Pi}], 
     Polygon[{{0, 3/4}, {0, 1/4}, {1/4, 0}, {3/4, 0}, {1, 1/4}, {1, 
        3/4}, {1/2, 1/4}}], Black, Line[{{0, 1/4}, {1/4, 0}}], 
     Line[{{1/4, 1/2}, {3/4, 0}, {1/2, 1/4}}], 
     Line[{{1/2, 1/4}, {1, 3/4}}], Line[{{3/4, 0}, {1, 1/4}}], 
     Line[{{0, 1/4}, {1/4, 1/2}}], 
     Circle[{1/2, 1/4}, Sqrt[2] 1/4, {Pi/4, 3/4 Pi}], 
     Circle[{1/2, 1/4}, Sqrt[2] 1/2, {Pi/4, 3/4 Pi}]},
   s1 = {Line[{{0, 1/4}, {1/2, 3/4}}], Line[{{0, 3/4}, {1/4, 1}}]}, 
   p1 = Polygon[{{0, 0}, {1/4, 0}, {0, 1/4}}]},
  With[{z = Rotate[q, 90 \[Degree], {1/2, 1/2}], 
    x = Rotate[w, 180 \[Degree], {1/2, 1/2}], 
    s = {LightCyan, 
      Polygon[{{0, 1/4}, {0, 3/4}, {1/4, 1}, {3/4, 1}, {1, 3/4}, {1, 
         1/4}, {3/4, 0}, {1/4, 0}}], White, 
      Polygon[{{1/4, 1/2}, {1/2, 1/4}, {3/4, 1/2}, {1/2, 3/4}}], p1, 
      Rotate[p1, 90 \[Degree], {1/2, 1/2}], 
      Rotate[p1, 180 \[Degree], {1/2, 1/2}], 
      Rotate[p1, -90 \[Degree], {1/2, 1/2}], Black, s1, 
      Rotate[s1, 90 \[Degree], {1/2, 1/2}], 
      Rotate[s1, 180 \[Degree], {1/2, 1/2}], 
      Rotate[s1, -90 \[Degree], {1/2, 1/2}]}, 
    a = Rotate[w, 90 \[Degree], {1/2, 1/2}], 
    d = Rotate[w, -90 \[Degree], {1/2, 1/2}], 
    c = Rotate[q, 180 \[Degree], {1/2, 1/2}], 
    e = Rotate[q, -90 \[Degree], {1/2, 1/2}]}, {z, 
    Table[Translate[x, {i, 0}], {i, 1, b - 2}], 
    Translate[c, {b - 1, 0}], 
    Table[Translate[{a, Table[Translate[s, {i, 0}], {i, 1, b - 2}], 
       Translate[d, {b - 1, 0}]}, {0, j}], {j, 1, h - 2}], 
    Translate[{q, Table[Translate[w, {i, 0}], {i, 1, b - 2}], 
      Translate[e, {b - 1, 0}]}, {0, h - 1}]}]]

Graphics[CelticBraid[7, 2]]

gives: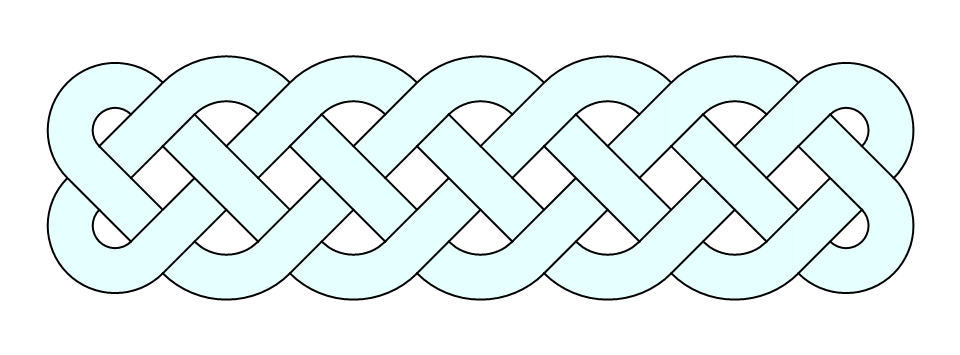

Graphics[CelticBraid[11, 3]]

gives: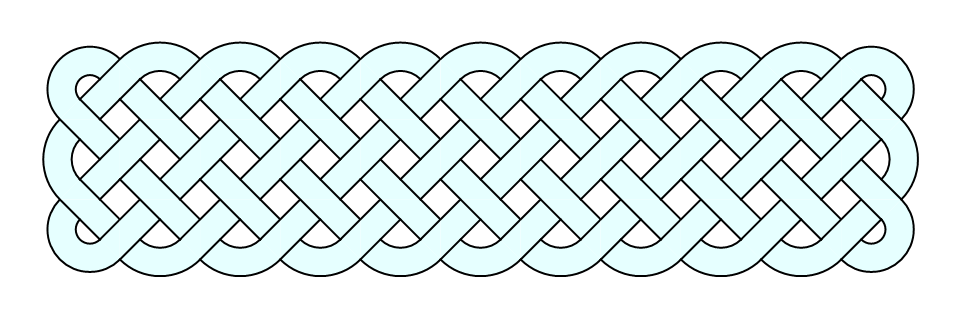

Graphics[CelticBraid[5, 5]]

gives: