First we set up the elements:
PSEelements[list_, col_] :=
Map[Item[Style[#, FontFamily -> "Ink Free"], Background -> col,
Frame -> Black] &, list]
s = LightRed; p = LightYellow; d = LightBlue; f = LightGreen;
S1 = PSEelements[{"H", "He"}, s];
S2 = PSEelements[{"Li", "Be"}, s];
P2 = PSEelements[{"B", "C", "N", "O", "F", "Ne"}, p];
S3 = PSEelements[{"Na", "Mg"}, s];
P3 = PSEelements[{"Al", "Si", "P", "S", "Cl", "Ar"}, p];
S4 = PSEelements[{"K", "Ca"}, s];
P4 = PSEelements[{"Ga", "Ge", "As", "Se", "Br", "Kr"}, p];
S5 = PSEelements[{"Rb", "Sr"}, s];
P5 = PSEelements[{"In", "Sn", "Sb", "Te", "I", "Xe"}, p];
S6 = PSEelements[{"Cs", "Ba"}, s];
P6 = PSEelements[{"Tl", "Pb", "Bi", "Po", "At", "Rn"}, p];
S7 = PSEelements[{"Fr", "Ra"}, s];
P7 = PSEelements[{"Nh", "Fl", "Mc", "Lv", "Ts", "Og"}, p];
D3 = PSEelements[{"Sc", "Ti", "V", "Cr", "Mn", "Fe", "Co", "Ni", "Cu",
"Zn"}, d];
D4 = PSEelements[{"Y", "Zr", "Nb", "Mo", "Tc", "Ru", "Rh", "Pd", "Ag",
"Cd"}, d];
D5 = PSEelements[{"La", "Hf", "Ta", "W", "Re", "Os", "Ir", "Pt", "Au",
"Hg"}, d];
D6 = PSEelements[{"Ac", "Rf", "Db", "Sg", "Bh", "Hs", "Mt", "Ds",
"Rg", "Cn"}, d];
F4 = PSEelements[{"Ce", "Pr", "Nd", "Pm", "Sm", "Eu", "Gd", "Tb",
"Dy", "Ho", "Er", "Tm", "Yb", "Lu"}, f];
F5 = PSEelements[{"Th", "Pa", "U", "Np", "Pu", "Am", "Cm", "Bk", "Cf",
"Es", "Fm", "Md", "No", "Lr"}, f];
all = Join[S1, S2, P2, S3, P3, S4, D3, P4, S5, D4, P5, S6, D5, F4, P6,
S7, D6, F5, P7];
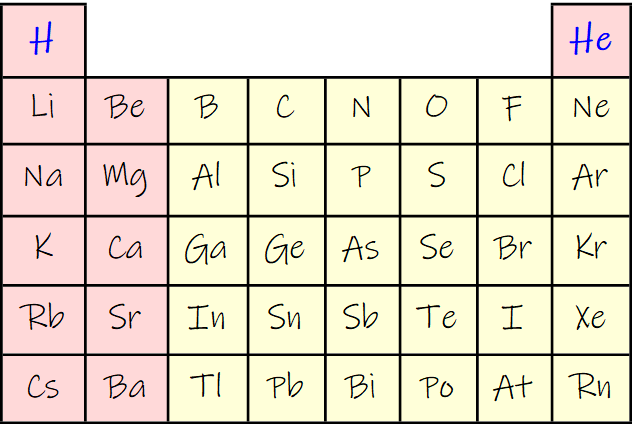
Then a simple eight column PSE is constructed (highlighting H an He):
Grid[PSE8 = {Join[{First[S1]}, Table["", 6], {Last[S1]}],
Join[S2, P2], Join[S3, P3], Join[S4, P4], Join[S5, P5],
Join[S6, P6]}, Spacings -> {1, 1},
ItemStyle -> {Automatic,
Automatic, {{1, 1} -> Directive[Bold, Blue], {1, 8} ->
Directive[Bold, Blue]}}]
Which gives:
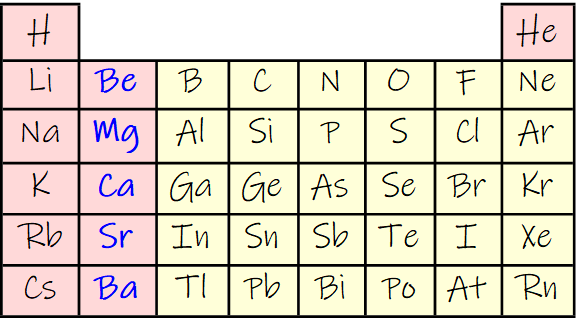
And now highlighting the Alkaline earth elements:
Grid[PSE8,
ItemStyle -> {Automatic, Automatic,
Table[{i, 2} -> Directive[Bold, Blue], {i, 2, 7}]}]
Looks like:
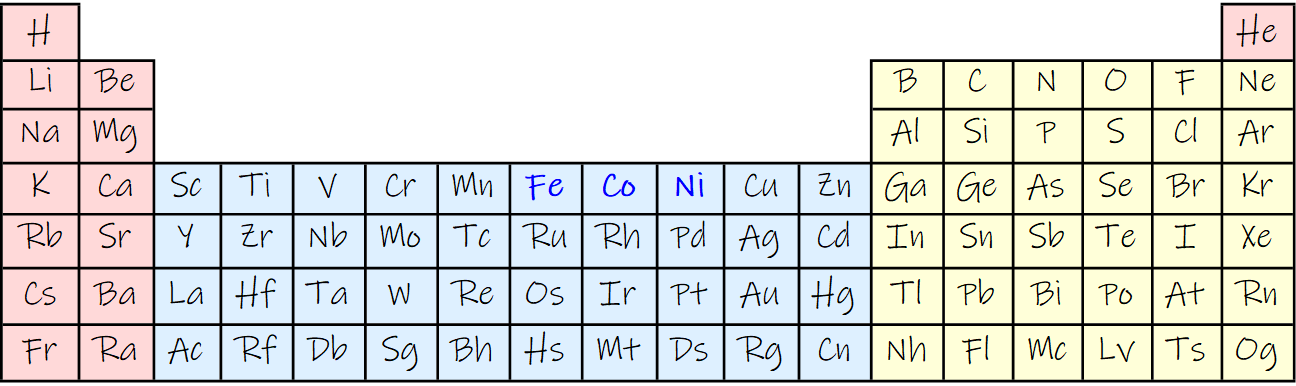
Here we have a standard 18 column PSE with ferromagnetic elements highlighted:
Grid[PSE18 = {Join[{S1[[1]]}, Table["", 6 + 10], {S1[[2]]}],
Join[S2, Table["", 10], P2], Join[S3, Table["", 10], P3],
Join[S4, D3, P4], Join[S5, D4, P5], Join[S6, D5, P6],
Join[S7, D6, P7]},
ItemStyle -> {Automatic, Automatic,
Table[{4, i} -> Directive[Bold, Blue], {i, 8, 10}]}]
gives:
A full PSE with still 18 columns and all elements without stable isotope marked:
Grid[PSE18full =
Join[PSE18, {Table["", 6 + 10 + 14], Join[Table["", 3], F4],
Join[Table["", 3], F5]}],
ItemStyle -> {Automatic, Automatic,
Join[{{5, 7} -> Directive[Red, Bold], {9, 7} ->
Directive[Red, Bold]},
Table[{6, i} -> Directive[Red, Bold], {i, 15, 18}],
Table[{7, i} -> Directive[Red, Bold], {i, 1, 18}],
Table[{10, i} -> Directive[Red, Bold], {i, 4, 17}]]}]
I never noticed before that there is no stable isotope for Pm:
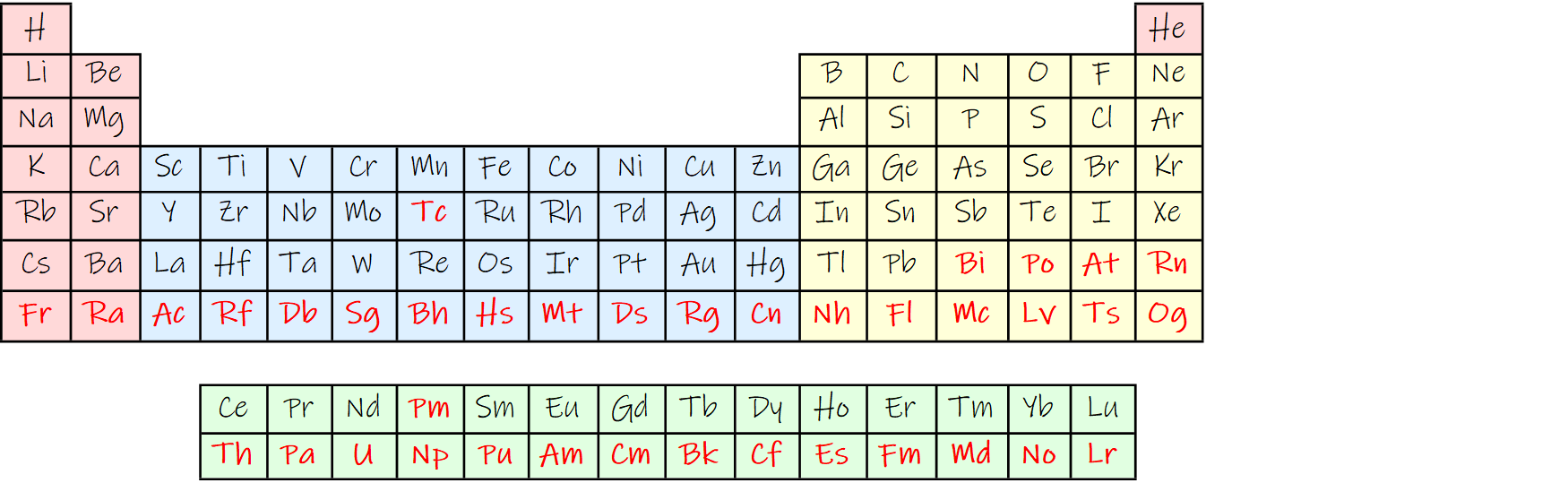
alternatively:
Grid[{Join[{S1[[1]]}, Table["", 6 + 10], {S1[[2]]}],
Join[S2, Table["", 10], P2], Join[S3, Table["", 10], P3],
Join[S4, D3, P4], Join[S5, D4, P5], Join[S6, {""}, Rest[D5], P6],
Join[S7, {""}, Rest[D6], P7], Table["", 6 + 10 + 14],
Join[Table["", 2], {First[D5]}, F4],
Join[Table["", 2], {First[D6]}, F5]},
ItemStyle -> {Automatic, Automatic,
Join[{{5, 7} -> Directive[Red, Bold], {9, 7} ->
Directive[Red, Bold]},
Table[{6, i} -> Directive[Red, Bold], {i, 15, 18}],
Table[{7, i} -> Directive[Red, Bold], {i, 1, 18}],
Table[{10, i} -> Directive[Red, Bold], {i, 3, 17}]]}]
gives:
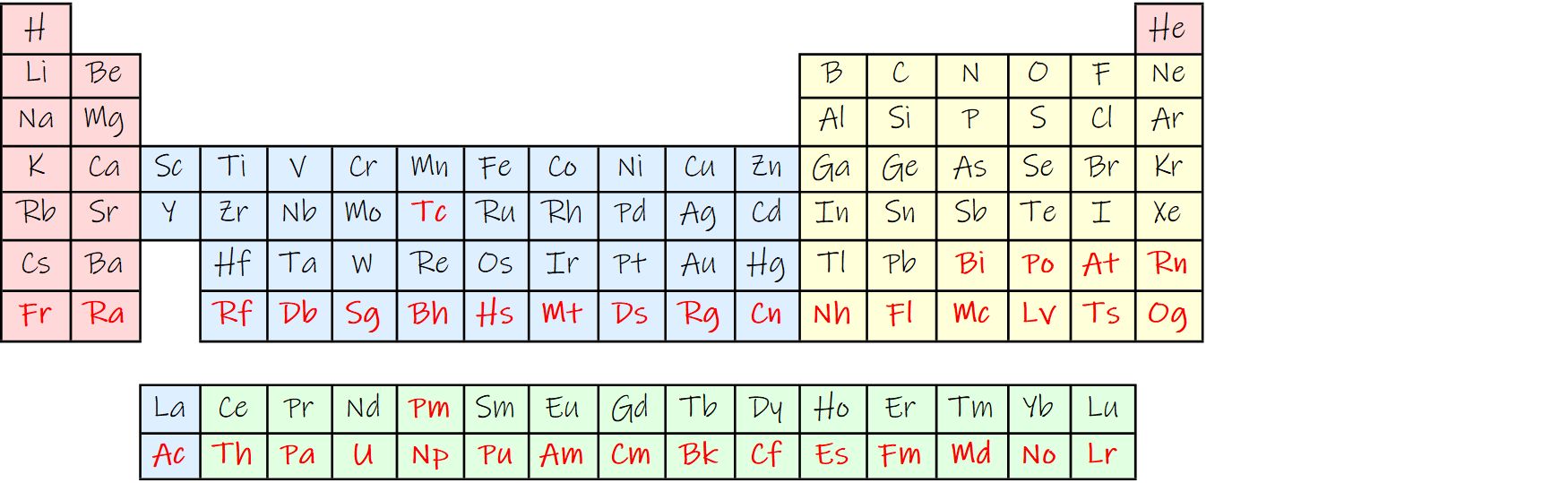
and a 32 column layout:
Grid[PSE32 = {Join[{S1[[1]]}, Table["", 6 + 10 + 14], {S1[[2]]}],
Join[S2, Table["", 10 + 14], P2], Join[S3, Table["", 10 + 14], P3],
Join[S4, {First[D3]}, Table["", 14], Rest[D3], P4],
Join[S5, {First[D4]}, Table["", 14], Rest[D4], P5],
Join[S6, {First[D5]}, F4, Rest[D5], P6],
Join[S7, {First[D6]}, F5, Rest[D6], P7]}, Spacings -> {0.5, 0.5},
ItemStyle -> {Automatic, Automatic,
Join[{{5, 21} -> Directive[Red, Bold], {6, 7} ->
Directive[Red, Bold]},
Table[{6, i} -> Directive[Red, Bold], {i, 29, 32}],
Table[{7, i} -> Directive[Red, Bold], {i, 1, 32}],
Table[{10, i} -> Directive[Red, Bold], {i, 4, 17}]]}]
gives:

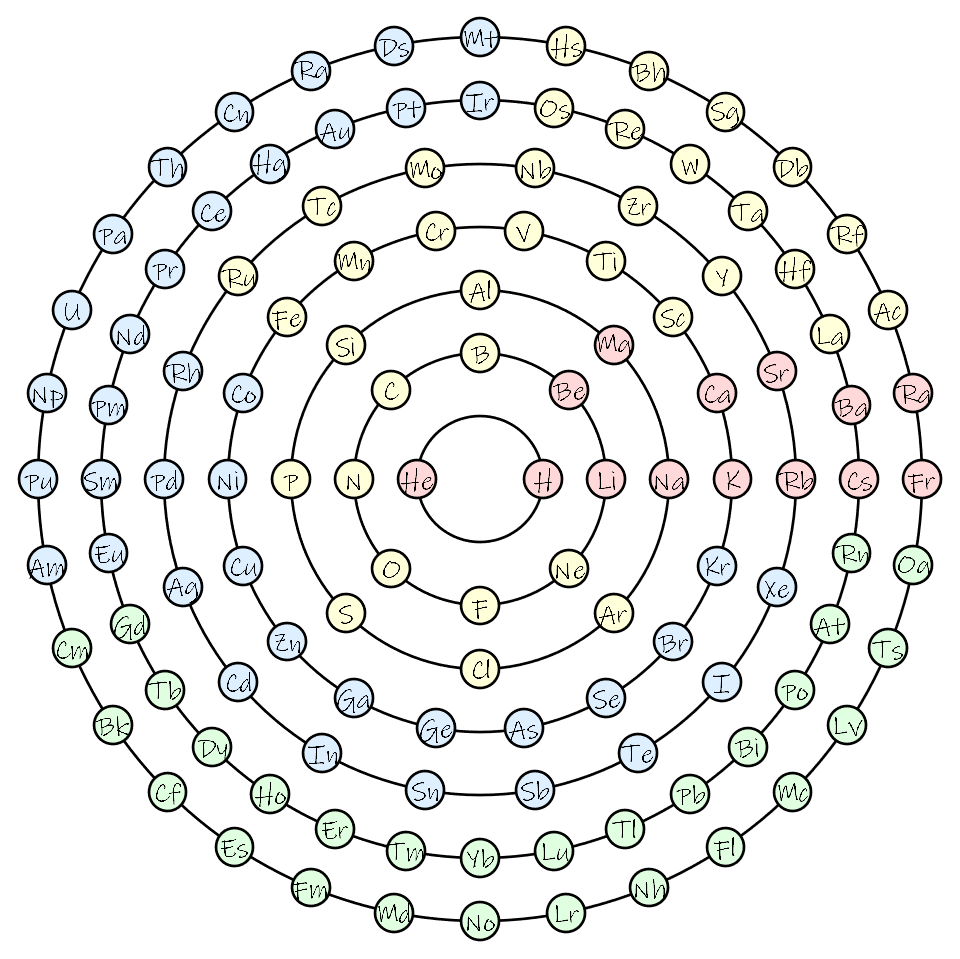
and finally a more artistic PSE view:
r = 0.3; Graphics[{
(*n=1*)
Circle[{0, 0}, 1],
shell = CirclePoints[2]; {LightRed, EdgeForm[Black],
Map[Disk[#, r] &, shell]}, {MapIndexed[Text[all[[#2[[1]]]], #1] &,
shell]},
(*n=2*)
Circle[{0, 0}, 2],
shell = CirclePoints[{2, 0 \[Degree]}, 8]; {LightRed,
EdgeForm[Black], Map[Disk[#, r] &, Take[shell, 2]], LightYellow,
Map[Disk[#, r] &, Take[shell, -6]]}, {MapIndexed[
Text[all[[#2[[1]] + 2]], #1] &, shell]},
(*n=3*)
Circle[{0, 0}, 3],
shell = CirclePoints[{3, 0 \[Degree]}, 8]; {LightRed,
EdgeForm[Black], Map[Disk[#, r] &, Take[shell, 2]], LightYellow,
Map[Disk[#, r] &, Take[shell, -6]]}, {MapIndexed[
Text[all[[#2[[1]] + 2 + 8]], #1] &, shell]},
(*n=4*)
Circle[{0, 0}, 4],
shell = CirclePoints[{4, 0 \[Degree]}, 18]; {LightRed,
EdgeForm[Black], Map[Disk[#, r] &, Take[shell, 2]], LightYellow,
Map[Disk[#, r] &, Take[shell, {3, 8}]], LightBlue,
Map[Disk[#, r] &, Take[shell, -10]]}, {MapIndexed[
Text[all[[#2[[1]] + 2 + 2 8]], #1] &, shell]},
(*n=5*)
Circle[{0, 0}, 5],
shell = CirclePoints[{5, 0 \[Degree]}, 18]; {LightRed,
EdgeForm[Black], Map[Disk[#, r] &, Take[shell, 2]], LightYellow,
Map[Disk[#, r] &, Take[shell, {3, 8}]], LightBlue,
Map[Disk[#, r] &, Take[shell, -10]]}, {MapIndexed[
Text[all[[#2[[1]] + 2 + 2 8 + 18]], #1] &, shell]},
(*n=6*)
Circle[{0, 0}, 6],
shell = CirclePoints[{6, 0 \[Degree]}, 32]; {LightRed,
EdgeForm[Black], Map[Disk[#, r] &, Take[shell, 2]], LightYellow,
Map[Disk[#, r] &, Take[shell, {3, 8}]], LightBlue,
Map[Disk[#, r] &, Take[shell, {9, 18}]], LightGreen,
Map[Disk[#, r] &, Take[shell, -14]]}, {MapIndexed[
Text[all[[#2[[1]] + 2 + 2 8 + 2 18]], #1] &, shell]},
(*n=7*)
Circle[{0, 0}, 7],
shell = CirclePoints[{7, 0 \[Degree]}, 32]; {LightRed,
EdgeForm[Black], Map[Disk[#, r] &, Take[shell, 2]], LightYellow,
Map[Disk[#, r] &, Take[shell, {3, 8}]], LightBlue,
Map[Disk[#, r] &, Take[shell, {9, 18}]], LightGreen,
Map[Disk[#, r] &, Take[shell, -14]]}, {MapIndexed[
Text[all[[#2[[1]] + 2 + 2 8 + 2 18 + 32]], #1] &, shell]}}]
PSE in circles: