I am dealing with a function / equation of a particular physical system and I want to find the En value of that equation. The equation is a transcendental complex equation whose expression is given by
T=(exp(0.04*i*q)/16*A^2*B*G)*(((A+G)^2*((A+B)^2*exp(2*i*(-0.01*k-0.01*p))-(A-B)^2*exp(-2*i*(-0.01*k-0.01*p))))+((A-G)^2*((A-B)^2*exp(-2*i*(-0.01*k+0.01*p))-(A+B)^2*exp(2*i*(-0.01*k+0.01*p))))+2*(A^2-B^2)*(A^2-G^2)*(exp(0.02*i*p)-exp(-0.02*i*p)))
with value of variable
m=h=1
c=137.036
Va=0
Vb=50000
p=(sqrt((En+m*c^2-Va)*(En-m*c^2-Va)))/(h*c)
q=(sqrt((En+m*c^2-Vb)*(En-m*c^2-Vb)))/(h*c)
k=(sqrt(En^2+m^2*c^4))/(h*c)
A=h*c*k/(En+m*c^2)
B=h*c*p/(En+m*c^2-Vb)
G=h*c*q/(En+m*c^2-Va)
In clearer form, the above equation looks like the following picture

where a=0.01 and b=0.02.
I tried to solve it using the formula Solve, NSolve, and also FindRoot. However, when using Solve and NSolve, the result is only the substitution of the known values into the equation, not the En value. And, when I try to finish using the FindRoot formula, the results are as below
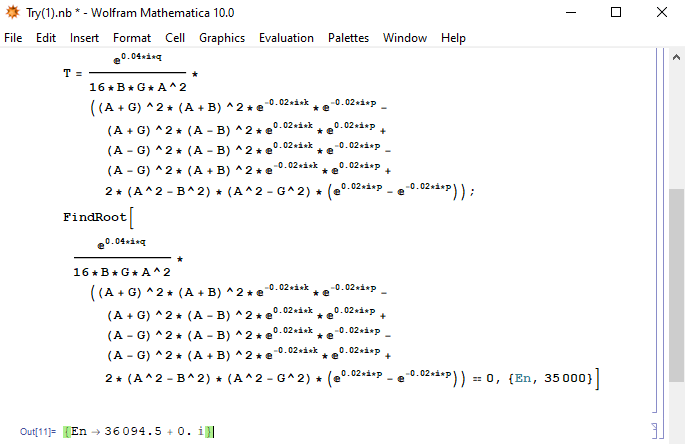
The 35000 number that I wrote in the FindRoot formula is a random number that I chose and the results are as shown in the picture.
Did I take the right steps? I think it's still wrong. I don't know and I am confused about what formula to use and how the steps should be. So, I would really appreciate if someone could give me a hint on how to get these solutions for En from the transcendental complex equation.
Thank you in advance.