Log of the likelihood and AIC in LinearModelFit
This is a follow-up to a question asked 5 years ago and which has had some recent activity: https://community.wolfram.com/groups/-/m/t/773607.
The question is about how AIC is calculated in LinearModelFit. LinearModelFit at best uses a non-standard formula and possibly the wrong log likelihood. Below I describe what those functions use to calculate AIC and what the more standard formulas are. (I concentrate only on AIC although the same issues likely affect BIC.)
These potential errors are not due to issues of numerical precision that can differ among software packages and hardware platforms. The issues are either wrong formulas or non-standard definitions (which either way are still undocumented in Mathematica).
Consider the following data in the documentation for LinearModelFit:
data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
Now use LinearModelFit and find the estimated variance and AIC value.
x =.;
lm = LinearModelFit[data, x, x];
lm["EstimatedVariance"]
(* 0.813559 *)
lm["AIC"]
(* 14.5262 *)
lm["ANOVATable"]
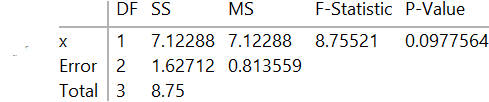lm["BestFitParameters"] (* {0.186441, 0.694915} *) The AIC value differs from what SAS and R produce from the same data and model. 
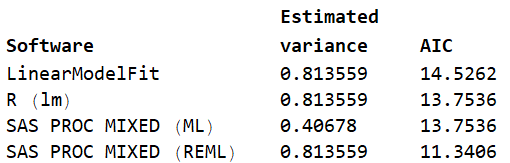Note that the AIC value from LinearModelFit does not match with any of the more standard values. Why all the differences? First, SAS PROC MIXED (ML) produces the maximum likelihood estimate of the variance: 0.40678. All of the others produce the REML estimate of variance which is the unbiased estimate of variance. That explains the differences in the estimated variance.
Explaining the differences in the AIC values is a bit more involved. The are two log likelihoods to consider: one for the maximum likelihood (ML) method and another for the restricted maximum likelihood method (REML). The REML method results in unbiased estimates of the variance components (which in this simpler model is just a single variance). (Think of the estimation of a sample variance. Dividing the sum of squares by n gives the biased maximum likelihood estimate. Dividing by n-1 gives the unbiased (REML) estimate.)
So AIC under maximum likelihood requires one to plug in the maximum likelihood estimate of variance into the log of the (unrestricted) likelihood. Both R (using lm) and SAS (using PROC MIXED with the ML method) do that. For the REML method in PROC MIXED from SAS the REML estimate of variance is used with the REML log likelihood.
But LinearModelFit plugs in the REML estimate of variance to the unrestricted log likelihood to obtain AIC. At best, that is not commonly done. At worst, it's wrong.
Here is how to duplicate the various calculations of AIC using the maximum likelihood and REML equations found in "Selecting the Best Linear Mixed Model under REML" by Matthew J. Gurka, The American Statistician, Feb. 2006, Vol. 60, No.1, Feb., 2006, pp. 19-26. The formulas for the log likelihood functions simplify greatly when there just a single error term and those simplified equations are given below.
(* Define data and model in "matrix" terms *)
n = Length[data];(* Sample size *)
x = Transpose[{ConstantArray[1, n], data[[All, 1]]}]; (* Design matrix *)
y = data[[All, 2]]; (* Response variable *)
\[Beta] = {intercept, slope}; (* Names of regression coefficients *)
p = Dimensions[x][[2]]; (* Number of fixed effect parameters *)
k = 1; (* Number of variance parameters *)
(* Estimates of standard deviations *)
\[Sigma]ML = Sqrt[lm["EstimatedVariance"]*(n - p)/n] ; (* Maximum likelihood estimate *)
\[Sigma]REML = Sqrt[lm["EstimatedVariance"]]; (* REML estimate *)
(* Log of unrestricted likelihood: maximum likelihood approach (ML) *)
logLML = -(n/2) Log[2 \[Pi]] - n Log[\[Sigma]] - (1/2) Transpose[y -x . \[Beta]] . (y - x . \[Beta])/\[Sigma]^2;
(* Log of restricted likelihood: REML approach *)
logLREML = -((n - p)/2) Log[2 \[Pi] \[Sigma]^2] - (1/2) Transpose[y - x . \[Beta]] . (y - x . \[Beta])/\[Sigma]^2;
(* Restricted log likelihood that SAS uses for REML: a constant term is removed from logLREML *)
logLREMLSAS = -((n - p)/2) Log[2 \[Pi]] - (n - p) Log[\[Sigma]] - (1/2) Log[Det[Transpose[x] . x]] -
(1/2) Transpose[y - x . \[Beta]] . (y - x . \[Beta])/\[Sigma]^2;
(* AIC values *)
aicML = -2 logLML + 2 (p + k) /. Thread[\[Beta] -> lm["BestFitParameters"]] /. \[Sigma] -> \[Sigma]ML
(* 13.7536 *)
aicREML = -2 logLREML + 2 k /. Thread[\[Beta] -> lm["BestFitParameters"]] /. \[Sigma] -> \[Sigma]REML
(* 7.26308 *)
aicREMLSAS = -2 logLREMLSAS + 2 k /. Thread[\[Beta] -> lm["BestFitParameters"]] /. \[Sigma] -> \[Sigma]REML
(* 11.3406 *)
aicLinearModelFit = -2 logLML + 2 (p + k) /. Thread[\[Beta] -> lm["BestFitParameters"]] /. \[Sigma] -> \[Sigma]REML
(* 14.5262 *)
So LinearModelFit takes the REML estimate of variance and plugs that value into the log of the unrestricted likelihood equation when it should either plug in that REML estimate of variance into the log of the restricted likelihood or plug in the maximum likelihood estimate of variance into the log of the unrestricted likelihood equation.
Attachments:
