A snark is a type of graph.
- Each vertex is connected to 3 others
- If a vertex and its 3 edges are removed, the graph is still connected
- If you color the edges with 3 colors, there will be a vertex with two edges of the same color
- You can color the edges with 4 colors so that no vertex has two edges of the same color
The first condition is called '3-regular'. The second is called 'bridgeless'. The last two are summed up by 'chromatic index 4'.
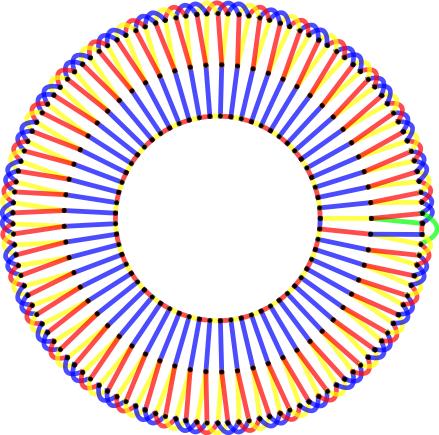
Snarks are interesting for many reasons. For quite some time, we only knew of a few examples. We still don't know all of them (or we do know all of them, but haven't realized it). In 1975 Rufus Isaacs found 'flower snarks', one for each odd number. They look like this
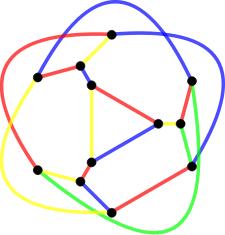 ,
,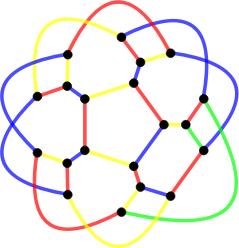 ,
,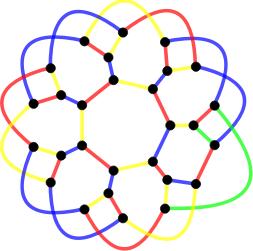 ,
,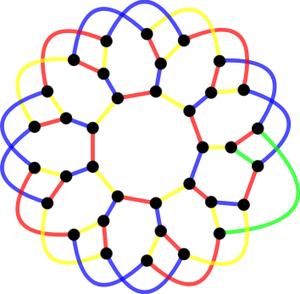
It's not hard to see that these are 3-regular and bridgeless. Chromatic index 4 is harder. I've colored the edges with 4 colors (and this isn't the only way to do so). But to be convinced, you also need to understand why 3 colors do not suffice -- no single illustration can do that.
I have, of course, created these images with Mathematica. My code categorizes the edges as 'core, spoke, stamen or petal'. Mathematica has many useful GraphLayouts to draw graph vertices and edges in sensible, pleasing ways. However, since we don't even know of all the snarks yet, how could we possibly expect to have GraphLayouts which work well for them!
I explicitly state the positions of the verties in a circle, as well as the curvatures of the petal edges. Finally, I include a verbose way of coloring the edges which you can prove is valid. It kills me that Mathematica can't (seamlessly) create svg from Graphs and Plots: this should be a very basic feature.It turns out svg and eps usually exports smartly (more than just embedding images). For some 3d plots, it falls back to an image (understandable since lighting is hard to reproduce with simple gradients).
If you know how to put this code in a web embeddable way, please let me know! Online notebooks don't seem to work once exported.
flowersnarkclassifyinternal[i_Integer /; 0 <= i < 4,
j_Integer /; 0 <= j < 4] :=
If[i == j == 0, "core",
If[SubsetQ[{i, j}, {0, 1}], "spoke",
If[SubsetQ[{i, j}, {1, 2}], "lstamen",
If[SubsetQ[{i, j}, {1, 3}], "rstamen",
If[i == j == 2, "lpetal",
If[i == j == 3, "rpetal", "idk"]]]]]];
flowersnarkclassify[i_Integer, j_Integer, n_Integer] :=
If[i == j, "idk",
If[SubsetQ[{Mod[i, 4 n], Mod[j, 4 n]}, {4 n - 2, 3}], "lpetal",
If[SubsetQ[{Mod[i, 4 n], Mod[j, 4 n]}, {4 n - 1, 2}], "rpetal",
flowersnarkclassifyinternal[Mod[i, 4], Mod[j, 4]]]]];
flowersnarkvertposs[n_Integer /; OddQ@n \[And] n >= 3] :=
Join @@ Table[{{Cos[(2 \[Pi] i)/n],
Sin[(2 \[Pi] i)/n]}, {1.5 Cos[(2 \[Pi] i)/n],
1.5 Sin[(2 \[Pi] i)/n]}, {2 Cos[(2 \[Pi] i)/n - 1.5/n],
2 Sin[(2 \[Pi] i)/n - 1.5/n]}, {2 Cos[(2 \[Pi] i)/n + 1.5/n],
2 Sin[(2 \[Pi] i)/n + 1.5/n]}}, {i, 0, n - 1}];
flowersnarkedges[n_Integer /; OddQ@n \[And] n >= 3] :=
Join @@
Table[{4 i \[UndirectedEdge] Mod[4 i + 4, 4 n],
4 i \[UndirectedEdge] 4 i + 1, 4 i + 1 \[UndirectedEdge] 4 i + 2,
4 i + 1 \[UndirectedEdge] 4 i + 3,
Annotation[#[[1]],
EdgeShapeFunction -> {"CurvedArc", "Curvature" -> #[[2]]}] &[
If[4 i + 6 <
4 n, {4 i + 2 \[UndirectedEdge]
4 i + 6, -2}, {4 i + 2 \[UndirectedEdge] 3, 2 + 2/n}]],
Annotation[#[[1]],
EdgeShapeFunction -> {"CurvedArc", "Curvature" -> #[[2]]}] &[
If[4 i + 7 <
4 n, {4 i + 3 \[UndirectedEdge]
4 i + 7, -2}, {4 i + 3 \[UndirectedEdge] 2, 0}]]}, {i, 0,
n - 1}];
v0[i_Integer, j_Integer, n_Integer] := Min[Mod[i, 4 n], Mod[j, 4 n]];
v1[i_Integer, j_Integer, n_Integer] := Max[Mod[i, 4 n], Mod[j, 4 n]];
flowersnarkedgecolor[i_Integer, j_Integer, n_Integer] :=
Switch[flowersnarkclassify[i, j, n],
"core",
If[SubsetQ[{Mod[i/4, n], Mod[j/4, n]}, {0, n - 1}], Blue,
If[Mod[v0[i, j, n]/4, 2] == 0, Red, Yellow]],
"spoke",
If[MemberQ[{0, 4 n - 4}, v0[i, j, n]],
If[Mod[v0[i, j, n]/n, 2] == 0, Yellow, Red], Blue],
"lstamen", If[v0[i, j, n] == 1, Green, Yellow],
"rstamen", If[v1[i, j, n] == 4 n - 1, Blue, Red],
"lpetal",
If[SubsetQ[{Mod[i, 4 n], Mod[j, 4 n]}, {3, 4 n - 2}], Green,
If[Mod[(v0[i, j, n] - 2)/4, 2] == 0, Blue, Red]],
"rpetal",
If[v0[i, j, n] == 2, Red,
If[Mod[(v0[i, j, n] - 3)/4, 2] == 0, Blue, Yellow]]];
flowersnark[n_Integer, vertlabels_, edgelabels_, edgecolors_] :=
Graph[Range[4 n] - 1,
flowersnarkedges[n] /.
If[edgelabels, {a_ \[UndirectedEdge] b_ :>
Annotation[a \[UndirectedEdge] b,
EdgeLabels -> flowersnarkclassify[a, b, n]]}, {}] /.
If[edgecolors, {a_ \[UndirectedEdge] b_ :>
Style[a \[UndirectedEdge] b,
flowersnarkedgecolor[a, b, n]]}, {}],
VertexLabels -> If[vertlabels, Automatic, None],
VertexCoordinates -> flowersnarkvertposs@n,
EdgeStyle -> Thickness[.01], VertexStyle -> Black,
VertexSize -> .4];
Manipulate[flowersnark[n, False, False, True], {n, 3, 31, 2}]
Thanks for reading. Here's flower snarks on 4*31 and 4*61 vertices ,
,