You have a precision issue because your equations have some rapid transients.
L = 1000; PDEin := -2.4669065517374813*
Derivative[0, 1][Tfin][\[Tau], z] +
Derivative[1, 0][Tfin][\[Tau], z] ==
0.0001770831817216026*(-Tfin[\[Tau], z] + Tfo[\[Tau], z])
PDEo := 0.9327310058932085*Derivative[0, 1][Tfo][\[Tau], z] +
Derivative[1, 0][Tfo][\[Tau], z] ==
0.07577538961255041*(10 + 0.026*z - Tfo[\[Tau], z]) +
0.00006695469437122687*(Tfin[\[Tau], z] - Tfo[\[Tau], z])
IC := {Tfin[0, z] == 10 + 0.026*z, Tfo[0, z] == 10 + 0.026*z}
tA = NDSolve[
SetPrecision[{PDEin, PDEo, IC, Tfo[\[Tau], 0] == 10,
Tfin[\[Tau], L] == Tfo[\[Tau], L]}, 20], {Tfin, Tfo}, {\[Tau], 0,
3600}, {z, 0, L}, WorkingPrecision -> 20];
gives
Plot3D[Evaluate[{Tfin[t, z]} /. tA], {t, 0, 3000}, {z, 0, L},
PlotRange -> All]
To get
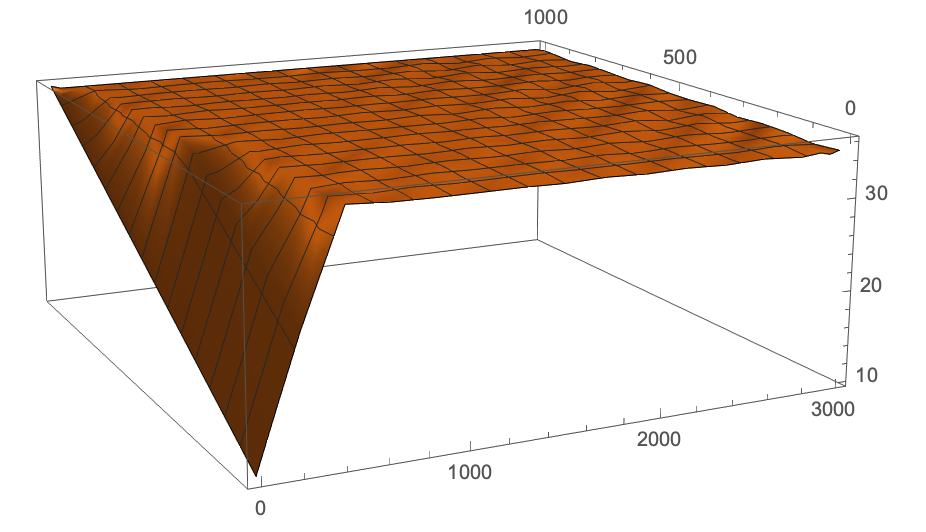
but you still get some "waviness" in the solution. I suggest you look at diving into the various settings for PDE solving using Method. Look at the settings in the documentation in Advanced Numerical Differential Equation Solving in the Wolfram Language if you need a better solution. You can also set the grid spacing, etc. there.
Regards,
Neil