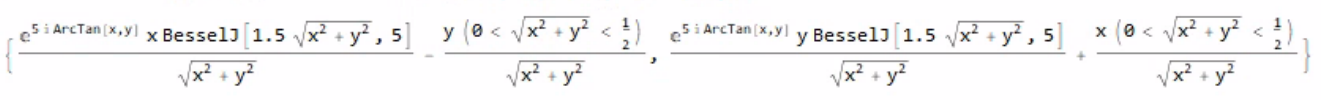Hi, I would like to convert the given function.
uA[r_, phi_] := {BesselJ[1.5 r, 5]*Exp[I 5 phi], 0 < r < 1/2};
to Cartesian form, but using
TransformedField["Polar" -> "Cartesian", uA[r, phi], {r, phi} -> {x, y}]
I get something weird, which does not look like a function. It seems the boundary part 0<r<1/2 disturbs the conversion process and generates a wrong output. Is there a better way to do this?
Thanks