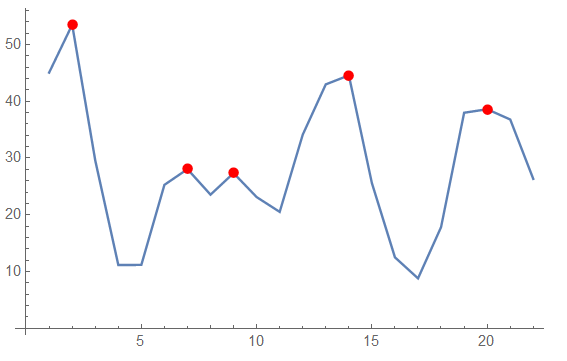
Hi,
We know that the value of the 20th peak point is 38.60.
If I want to estimate the position and also the value of this point based on previous peak points. How do I that?
data = {45.070711725125555`, 53.498297934722096`,
29.584510552747492`, 11.151690956807158`, 11.189625653415481`,
25.285839036082518`, 28.057908240982226`, 23.56037341335459`,
27.359877903104667`, 23.136393135264058`, 20.52783862787402`,
34.12780683174508`, 42.99141335930445`, 44.57290718131107`,
25.58296670347263`, 12.519024579537946`, 8.813650190806353`,
17.823927962891695`, 37.99345093666351`, 38.609478630177335`,
36.80195533249116`, 26.344280857176376`};
FindPeaks[data]
{{2, 53.4983}, {7, 28.0579}, {9, 27.3599}, {14,
44.5729}, {20, 38.6095}}
ListLinePlot[{data, FindPeaks[data]},
Joined -> {True, False},
PlotStyle -> {Automatic, {Red, PointSize[.02]}}]