Let's prove this statement in V.P. Maslov's book "Operational methods":
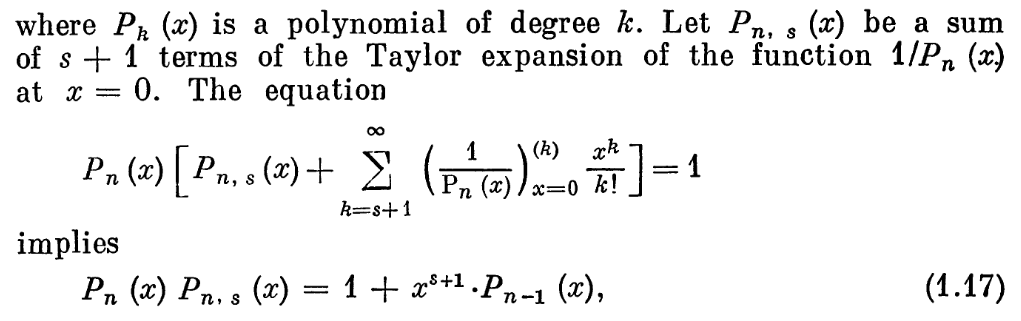
We can define the needed entities like this:
P[n_, x_] := Sum[a[k]*x^k, {k, 0, n}]
P[n_, s_, x_] := Normal[Series[1/P[n, x], {x, 0, s}]]
Now if we distribute the definitions like this:
DistributeDefinitions[Evaluate[Context[]]];
we can prove this theorem for any range of values of n and s (say 10 by 10 to begin with):
ParallelTable[{n, s,
Length[CoefficientList[(P[n, x]*P[n, s, x] - 1)/x^(s + 1), x]] ==
n}, {n, 1, 10}, {s, 1, 10}]
This works, i.e. all entries have True as the 3rd element. However, if we define our Ps like this, which looks much nicer in the frontend, using subscript indices:
Subscript[P, n_][x_] := Sum[Subscript[a, k]*x^k, {k, 0, n}]
Subscript[P, n_, s_][x_] := Normal[Series[1/Subscript[P, n][x], {x, 0, s}]]
Then we get the wrong result, namely some of the entries contain False instead of True:
ParallelTable[{n, s, Length[CoefficientList[(Subscript[P, n][x]*Subscript[P, n, s][x] -
1)/x^(s + 1), x]] == n}, {n, 1, 3}, {s, 1, 3}]
CoefficientList::poly : (-1+Subscript[P, 1][x] Subscript[P, 1,1][x])/x^2 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 2][x] Subscript[P, 2,1][x])/x^2 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 3][x] Subscript[P, 3,1][x])/x^2 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 1][x] Subscript[P, 1,2][x])/x^3 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 2][x] Subscript[P, 2,2][x])/x^3 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 3][x] Subscript[P, 3,2][x])/x^3 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 1][x] Subscript[P, 1,3][x])/x^4 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 2][x] Subscript[P, 2,3][x])/x^4 is not a polynomial.
CoefficientList::poly : (-1+Subscript[P, 3][x] Subscript[P, 3,3][x])/x^4 is not a polynomial.
General::stop : Further output of CoefficientList::poly will be suppressed during this calculation.
General::stop : Further output of CoefficientList::poly will be suppressed during this calculation.
General::stop : Further output of CoefficientList::poly will be suppressed during this calculation.
{{{1, 1, True}, {1, 2, True}, {1, 3, True}}, {{2, 1, False}, {2, 2,
False}, {2, 3, False}}, {{3, 1, False}, {3, 2, False}, {3, 3,
False}}}
But the non-parallel version of the same works fine:
Table[{n, s, Length[CoefficientList[(Subscript[P, n][x]*Subscript[P, n, s][x] -
1)/x^(s + 1), x]] == n}, {n, 1, 3}, {s, 1, 3}]
{{{1, 1, True}, {1, 2, True}, {1, 3, True}}, {{2, 1, True}, {2, 2,
True}, {2, 3, True}}, {{3, 1, True}, {3, 2, True}, {3, 3, True}}}
So, my guess is that with the subscript-index definitions one has to do something else to DistributeDefinitions[] properly? Tested on 11.3, 12.1 and 12.3 -- same problem on all versions.