I'm trying to solve a system of two equations, one of them is implicit. Using Solve[], I got 2 solutions. However, one of the solutions is not a point for one of the equations, and graphically, the two equations do not cross at the point. I'm confused how Mathematica considers it a solution when it only satisfy one of the equations. Notebook is attached. Here are the two equations, p and T are the only variables.
Equation 1:
p = \[Phi]/R + ((1 - \[Phi]) \[Phi] (1 - \[Lambda]) \[Beta])/(((W - p T) R + \[Phi] T) R + \[Phi] (1 - \[Phi]) T)/(R (\[Lambda]/((W - p T) R + \[Phi] T ) + ((1 - \[Lambda]) \[Beta] R)/(((W - p T) R + \[Phi] T) R + \[Phi] (1 - \[Phi]) T)))
Equation 2:
p = A/T
To solve the equations, I did:
Solve[p - \[Phi]/R - ((1 - \[Phi]) \[Phi] (1 - \[Lambda]) \[Beta])/(((W - p T) R + \[Phi] T) R + \[Phi] (1 - \[Phi]) T)/(R (\[Lambda]/((W - p T) R + \[Phi] T ) + ((1 - \[Lambda]) \[Beta] R)/(((W - p T) R + \[Phi] T) R + \[Phi] (1 - \[Phi]) T))) == 0 && p == A/T , {p, T}]
and the solutions are:
{{p -> -1.98998*10^-8, T -> -5.02518*10^9}, {p -> 0.319279, T -> 313.206}}
However, when I substituted T = -5.02518(10^9) into equation 1, I got {p -> 0.325402} instead of {p -> -1.9899810^-8}
T -> -5.02518*(10^9)
FindRoot[p - \[Phi]/R - ((1 - \[Phi]) \[Phi] (1 - \[Lambda]) \[Beta])/(((W - p T) R + \[Phi] T) R + \[Phi] (1 - \[Phi]) T)/(R (\[Lambda]/((W - p T) R + \[Phi] T ) + ((1 - \[Lambda]) \[Beta] R)/(((W - p T) R + \[Phi] T) R + \[Phi] (1 - \[Phi]) T))), {p, 0.2}]
output is {p -> 0.325402}
The parameter values are:
\[Beta] = 0.95
R = 1/\[Beta]
W = 1000000
A = 100
\[Phi] = 1/5
\[Lambda] = 0.1
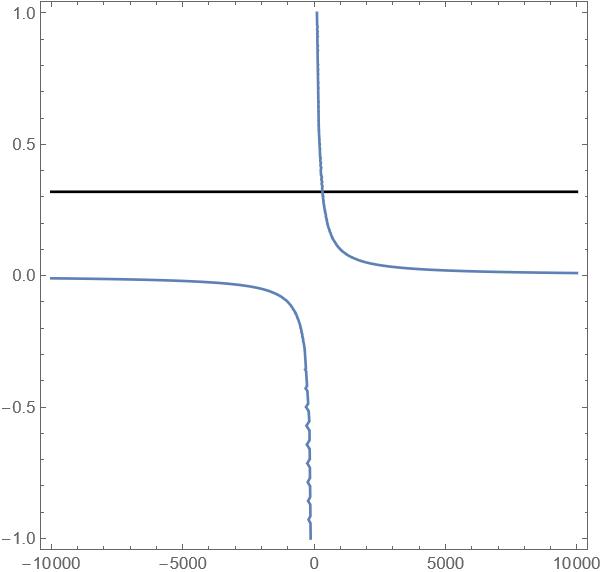
Does anyone know how the solution {p -> -0.0000199018, T -> -5.02466*10^6} was derived? It's a point on equation 2 but not equation 1. In the graph below I plotted both equations. p is the y-axis, T is the x-axis. The blue line is p = A/T, why does it look squiggly?
 Attachments:
Attachments: