Thank you guys, you're the boss we got it the expression, well something like that, this is the final code:
aa = ((sol = s /. Solve[s^2 + (R/L) s + 1/(L*C1) == 0, s] // Expand) /.
Sqrt[x__]/(a_*Sqrt[y_]) :> Sqrt[x/(y*a^2)]) /.
Sqrt[(x_ + y1_)/(y_*a_^2)] :> Sqrt[x/(y*a^2) + y1/(y*a^2)];
bb = aa /. Sqrt[x__] -> xx /. xx -> 2 yy /.
yy -> Sqrt[(-(4/(four*C1*L)) + R^2/(four*L^2))];
bb /. four -> "4"
and this is the final result:
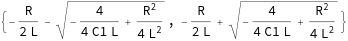
Finally I just put "four" as divisor, I'm new in this and you help me, thousand thanks to you guys it is what I want to do.
Note: where can I found more information about pure functions in wolfram or symbolic manipulation? the examples of Wolfram introduction are basics.