Here is an example where
ParallelTable is slower than
Table and yileds some weirdness.
I have tried to implement a Monte Carlo simulaiton for a stock price following a geometric brownian motion (the original function appears to be slow, probably because it contains more information than I need). And, stumbled upon some inexplicable, at first, results.
And so, let "s" be the vector of initial prices. The following is the simmulation:
s = 0 Range[10^5] + 100;
data = ParallelTable[s = s + r s dt + \[Sigma] s Sqrt[dt] RandomVariate[NormalDistribution[], 10^5], {i, 300}]; // AbsoluteTiming
data = data\[Transpose];
This takes
{6.219356, Null}
And if we dare to plot a few processes,
GraphicsRow[{ListLinePlot[data[[1, All]]], ListLinePlot[data[[;; 7, All]]]}]
we obtain:
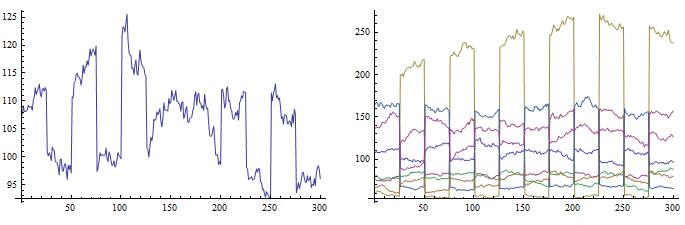
One might be happy that he gets jumps, without much effort. But this is not what it should look like.
When we use
Table instead it will take
{3.485199, Null} and the results are nicer:
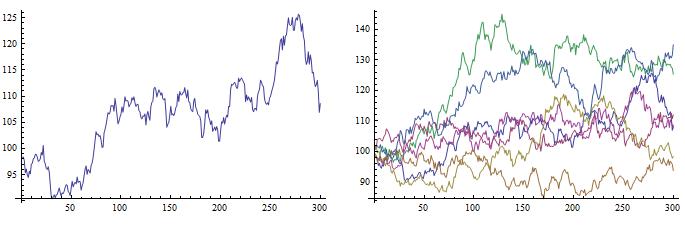
Even though there are "parallels" on the first graphs, it took me a while to figure out the reason.
I thought it's worth making a note,