I posted the question also here https://math.stackexchange.com/q/4217369/680634 . For some reason, the LaTeX does not compile here.

For my research, I must solve many integrals of the Owen's T function. As such, I am having struggles in calculating the integral \begin{equation} f(x, t) = \int_{0^{-}}^{t}d{s} \ e^{-(t+s)} \ \operatorname{T}\left(\frac{x}{\sqrt{2t}}, \sqrt{\frac{s}{2t-s}}\right). \end{equation}

I asked a similar question in [1] for the integral $$ \int_{0^{-}}^{t}d{s} \ \operatorname{T}\left(\frac{x}{\sqrt{2t}}, \sqrt{\frac{s}{2t-s}}\right), $$

which was beautifully answered. Nevertheless, if one follows the same procedure the exponential complicates things. What I have done until know is following [1] which yields

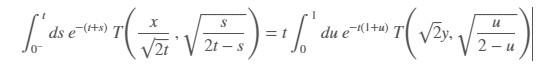
where we performed the change of variable $s=tu$ and took $y=\frac{x}{2\sqrt{t}}$. Substituting the definition for Owen's T function and using Tonelli theorem gives

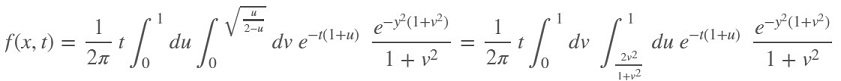
Taking the integral over u

$$ f(x,t)= \frac{1}{2\pi}t \int_{0}^{1} d{v} \ \frac{e^{-y^2(1+v^2)}}{1+v^2}\left(\frac{e^{\frac{2 t}{v^2+1}-3 t}}{t}-\frac{e^{-2 t}}{t}\right) = -\frac{1}{2\pi} e^{-2 t}\int{0}^{1} d{v} \ \frac{e^{-y^2(1+v^2)}}{1+v^2}+\frac{1}{2\pi} \int{0}^{1} d{v} \ \frac{e^{-y^2(1+v^2)}}{1+v^2}e^{\frac{2 t}{v^2+1}-3 t} $$

And using the definition of Owen T function gives \begin{equation} f(x, t)= -T\left(\tfrac{x}{\sqrt{2t}}, 1\right)e^{-2 t}+\frac{1}{2\pi} e^{-3t} \color{blue}{\int_{0}^{1} d{v} \frac{e^{-y^2(1+v^2)}}{1+v^2}e^{\frac{2 t}{v^2+1}}} \end{equation}

The Owen T term, i.e. the first term, can be written in terms of Error function. However, I am struggling in solving the integral in the second term. I have tried integrate by part, but this just yield a more complicated expression. Someone who knows a way forward?

Also I checked above calculation numerically and it indeed holds up!

In[270]:= ClearAll["Global`*"];
int1[x_, t_]:=-OwenT[x/Sqrt[2t],1]*Exp[-2t]+1/(2\[Pi])*Exp[-3t]*NIntegrate[ Exp[-(x/(2Sqrt[t]))^2*(1+v^2)]/(1+v^2)*Exp[(2t)/(1+v^2)], {v,0,1},WorkingPrecision->7] ;
int2[x_, t_]:=NIntegrate[Exp[-(t+s)]*OwenT[x/Sqrt[2t],Sqrt[s/(2t-s)]], {s,0,t},WorkingPrecision->7] ;
{x,t}=RandomReal[{0,1},2,WorkingPrecision->50]; 
int1[x, t]
int2[x, t]

Out[274]= 0.01602865
Out[275]= 0.01603027