Hello, I would like to solve the following PDE for Psi(x,y,z,t) 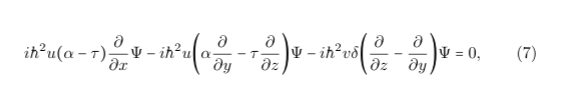
where alpha, tau, delta and u and v are the following 4-vectors:
alpha= [1,2,3,6] tau= [4,2,3,5] delta= [3,3,3,1] u=[0.1,0.5,0.3,0.5] v=[0.6,0.1,0.2,0.4]
and i is the imaginary unit, while hbar is the reduced Planck constant. The initial conditions are psi(0,0,0,0)=alphahbar and psi(1,1,1,1)=alphahbar*e^(x+y)
How can I set this up? So far I made only a template based test, but it seems very different situation than described on https://reference.wolfram.com/language/howto/SolveAPartialDifferentialEquation.html
So far I tried it without the vectors, as I am not sure how to import the vectors:
pde = D[psi[x, y,z,t],x] - D[psi[x, y,z,t],y]+D[psi[x, y,z,t],z]- D[psi[x, y,z,t],z]+D[psi[x, y,z,t],y] == 0
soln = DSolve[pde, psi[x,y,z,t], {x,y,z,t}]
Thank you