I wanted to share an application of Carl Woll's TensorSimplify/einsum utilities, which I first discovered here and I think should be known more widely.
There's a number of special formulas involving expectations of Gaussian variables, see section 20.5.2 of Seber "A Matrix Handbook for Statisticians". For instance, the following holds for a general matrix $A$ and $x$ distributed as zero-centered Gaussian with covariance $\Sigma$:
$$E[(x'Ax)^3]=\left[\text{trace}(A\Sigma)\right]^3 + 6\ \text{trace}(A\Sigma)\text{trace}\left[(A\Sigma)^2\right]+8\ \text{trace}\left[(A\Sigma)^3\right]$$
These was painstakingly derived by hand, but a more general and gentler approach is possible with Mathematica.
As a motivating example, I'll show how to use Mathematica to get a formula for $E[xx'Axx']$ which I needed for my work but couldn't find in textbooks.
Use Einstein's summation notation to write:
$$E[xx'Axx']_{il}=M_{ijkl}A_{jk}$$
Where $M_{ijkl}$ is the 4th moment tensor $E[x_i x_j x_k x_l]$
The next trick is the use Isserlis/Wicks Theorem. For centered Gaussian variable $x$, Isserlis theorem tells us that
$$E[x_i x_j x_k x_l]=E[x_i x_k]E[x_j x_l] +E[x_i x_l]E[x_j x_k]+ E[x_i x_j]E[x_k x_l] $$
Right-hand side of this formula is easier to remember in diagrammatic notation 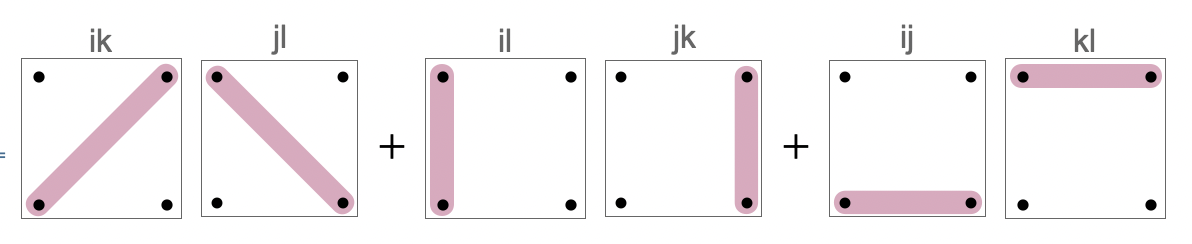
Now substitute this into original formula involving $M$ to get three different einsums, and use TensorSimplify package to obtain matrix expressions for each of them.
However, if we need non-centered Gaussian variables, Isserlis theorem doesn't apply. In such case, use Mathematica to derive a more general form of Isserlis.
Isserlis theorem is a special case of a general law linking cumulants and moments together - the general compositional formula (section 2.3.4 of McCullough book). This fundamental equation, linking moments and cumulants, is implemented in Mathematica's MomentConvert function.
To use this function here use the fact that cumulants of order above 2 are zero in a Gaussian. This property is the defining property of a Gaussian, and number "2" is special. This property is the reason why Gaussian expectations have nice algebraic expressions.
To use it in practice, use Mathematica's MomentConvert function to convert your target moment to cumulants, set to zero all cumulants above order 2, MomentConvert each of the cumulant terms back to moments, then Simplify. In our example involves 4th moment tensor $M_{ijkl}$ so we start with Moment[{1,1,1,1}], and get the following fourth moment formula in terms of first and second moments:
$$E[x_i x_j x_k x_l]=E[x_i x_j]E[x_k x_l] + E[x_i x_k]E[x_j x_l]+E[x_i x_l]E[x_j x_k]-2 E[x_i]E[x_j]E[x_k]E[x_l] $$
Equivalently in diagrammatic notation: 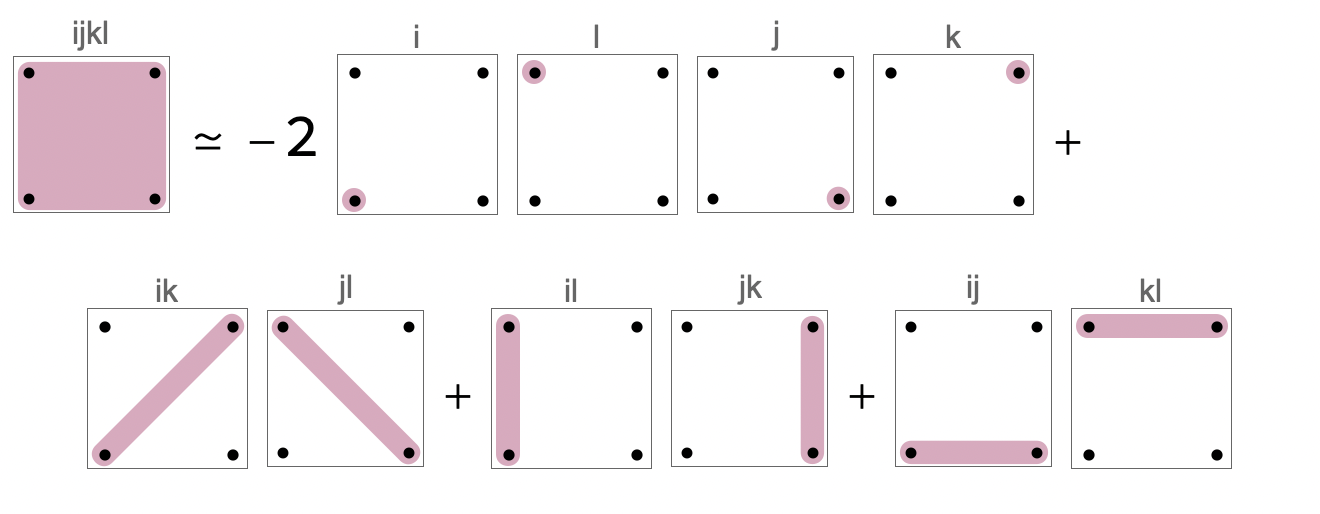
You can see that it is almost the Isserlis theorem for centered Gaussian, but with an extra correction term involving mean $E[x_i]=\mu$.
Now plug this formula into original einsum involving $M$, distribute summation to get 4 einsums, and use FromTensor from the TensorSimplify package to obtain matrix expressions for each of them.
For instance to get matrix expression for mean term, run this command: FromTensor@TensorReduce@ einsum[{{2, 3}, {1}, {2}, {3}, {4}} -> {1, 4}, A, mu, mu, mu, mu]; The result corresponds to the following identity:
$$\sum_{jk} A_{jk} \mu_i \mu_j \mu_k \mu_l=\mu^T A\mu (\mu\otimes \mu) $$
Running this for all 4 terms, we get the following formula
$$E[xx'Axx']=E[xx']AE[xx']+E[xx']A^T E[xx'] + E[xx'] \text{Tr}(A^T E[xx'])-2 \mu^T A\mu \mu\otimes \mu$$
As a correctness check, create a multivariate Gaussian with random integer parameters, use Expectation to compute expectations, and use Reduce to ensure exact equality with our formula.
This package saved me time in deriving formulas needed to obtain heuristics needed to properly set learning rate hyper-parameter for my neural network training experiments, here's a write-up of underlying theory.
Below are related useful identities I obtained using this approach (background: SE post,Google doc). $$ \begin{eqnarray} X^2&=&E[xx']\\ E[(xx')(xx')]&=&2X ^2+X^2 \text{Tr} X^2 -2\|\mu\|^2 \mu \mu'\\ E[(x'x)(xx')]&=&E[(xx')(xx')]\\ E[xx'\otimes xx']&=&2P_d( X^2\otimes X^2) + \text{vec} X^2 (\text{vec} X^2)'-2(\mu \mu')\otimes (\mu \mu')\\ E[\langle x, x\rangle^2]&=&2\text{tr}(X^2 X^2)+\text{tr}(X^2)^2-2\|\mu\|^4\\ E[\langle x, y\rangle^2]&=&\text{jointly Gaussian x,y: formula involving }E[xx'],E[yy'],E[xy'] \end{eqnarray} $$
This is a semi-automatic approach. A useful contribution would be a utility that could automatically derive such formulas (from this post and from Seber, Section 20.5)
 Attachments:
Attachments: