Last night in the chat room, the task of visualizing high-dimensional objects
was brought up. It seemed fun, so I wandered off into the computational universe in that direction to find a minimal, shareable result. The steps are:
- Define an object (points and edges)
- Generate some sliders to control rotation (choosing a number of perpendicular axes equal to the number of dimensions of the object is a good starting set)
- Generate a set of orthogonal projections by choosing all pairs of dimensions
This shows the popular
tesseract or 4-dimensional cube.
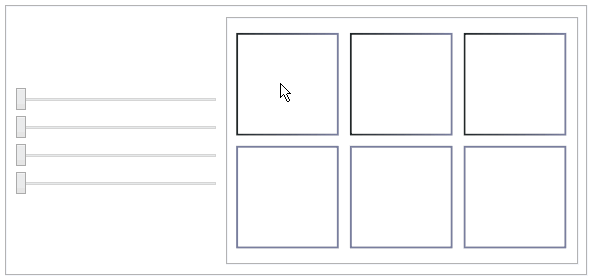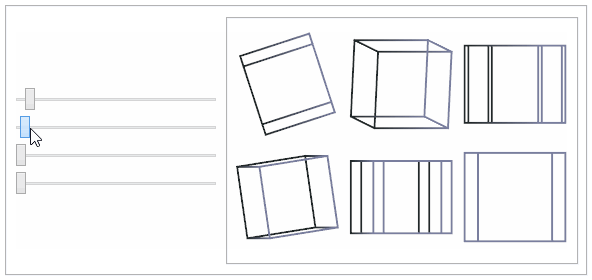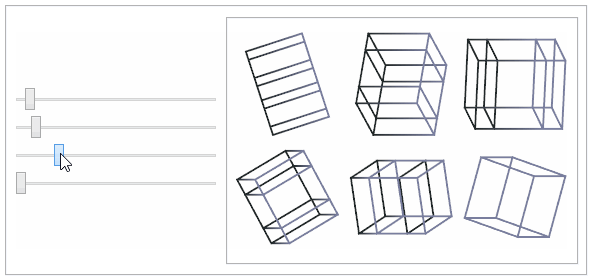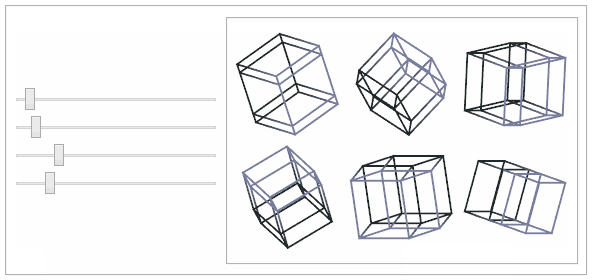
points = Tuples[{-1, 1}, 4];
edges = Select[Subsets[Range@Length@points, {2}],
Count[Subtract @@ points[[#]], 0] == 3 &];
colors = ColorData["AtlanticColors"] /@ Rescale@points[[All, 1]];
dimension = Length@First@points;
controls =
Column[(angle@# = 0; Slider[Dynamic@angle@#, {0, 2 Pi}]) & /@
Range@dimension];
views = Dynamic@
GraphicsGrid@
Partition[
Graphics[{Thick,
GraphicsComplex[#,
Line[edges, VertexColors -> (colors[[#]] & /@ edges)]]},
ImageSize -> {100, 100}] & /@
Outer[#2[[#]] &, Subsets[Range@dimension, {2}],
MapIndexed[RotationTransform[angle @@ #2, #] &,
Composition @@ Partition[IdentityMatrix@dimension, 2, 1, 1]]@
points, 1], 3, 3, 1, Null];
Panel@Row@{controls, Spacer@10, Panel@views}