Not there yet, but I can see patterns emerging which I'm hoping would allow me to make this to work without having to change the code.
Maybe using NestList?
Although it looks simpler to use the Mathematica PolynomialQuotient and PolynomialRemainder functions, for the sake of better understanding, I'd also like to calculate them myself. But I think I need some temporary variables in that case and I'm not sure where the best place to declare them would be.
I wish there were a simpler way to do this, with having to Pad the polynomials out with zeroes so they're the same length. Maybe converting them to strings. But then there's a tradeoff with the code becoming less intuitive.
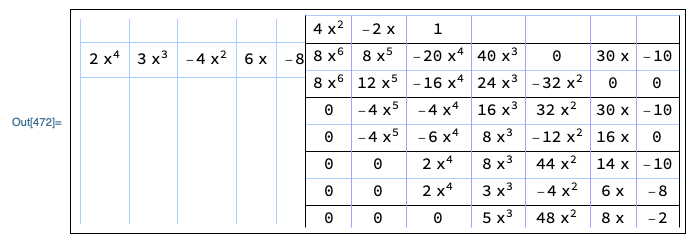
Row[{
Grid[
{{}, D}~Join~Table[{}, {i, 3, nCols}],
Dividers -> {
Table[i -> RGBColor[0.67, 0.8, 1.], {i, 1, d}],
{2 -> RGBColor[0.67, 0.8, 1.], 3 -> RGBColor[0.67, 0.8, 1.]}
},
Spacings -> {1, 1}
],
Grid[{
Q,
A,
pl[A[[1]]/D[[1]] D, a, 0, 2],
A - pl[A[[1]]/D[[1]] D, a, 0, 2],
pl[(A - pl[A[[1]]/D[[1]] D, a, 0, 2])[[2]]/D[[1]] D, a, 0, 1],
A - pl[A[[1]]/D[[1]] D, a, 0, 2] -
pl[(A - pl[A[[1]]/D[[1]] D, a, 0, 2])[[2]]/D[[1]] D, a, 0, 1],
pl[Q[[3]] D, a, 0],
A - pl[Q[[1]] D, a, 0, 2] - pl[Q[[2]] D, a, 0, 1] -
pl[Q[[3]] D, a, 0]
},
Dividers -> {
{1 -> RGBColor[1, 0, 0],
Table[i -> RGBColor[0.65, 0.62, 1.], {i, 2, a}]},
{1 -> RGBColor[0.67, 0.8, 1.], 2 -> GrayLevel[0],
3 -> RGBColor[0.67, 0.8, 1.], 4 -> GrayLevel[0],
5 -> RGBColor[0.67, 0.8, 1.], 6 -> GrayLevel[0],
7 -> RGBColor[0.67, 0.8, 1.], 8 -> GrayLevel[0]}
}
]},
Frame -> True]