Hi Jay,
Here is one way that I saw on MSE. I searched but cannot find it
ClearAll[x, y, x];
exp = 4 x y^2 z + 4 z^2 - 5 x^3 + 7 x^2 z^2
orders = MonomialList[exp, #] & /@ {"Lexicographic", "DegreeLexicographic",
"DegreeReverseLexicographic", "NegativeLexicographic",
"NegativeDegreeLexicographic", "NegativeDegreeReverseLexicographic"}
(* {{-5 x^3, 7 x^2 z^2, 4 x y^2 z, 4 z^2}, {7 x^2 z^2, 4 x y^2 z, -5 x^3,
4 z^2}, {4 x y^2 z, 7 x^2 z^2, -5 x^3, 4 z^2}, {4 z^2, 4 x y^2 z,
7 x^2 z^2, -5 x^3}, {4 z^2, -5 x^3, 7 x^2 z^2,
4 x y^2 z}, {4 z^2, -5 x^3, 4 x y^2 z, 7 x^2 z^2}} *)
Replace[orders, {x__} :> HoldForm[+x], 1]
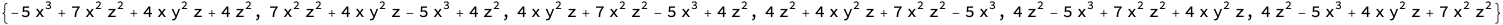
Shown as an image since it is a held expression and releasing the hold will revert to lexicographic.