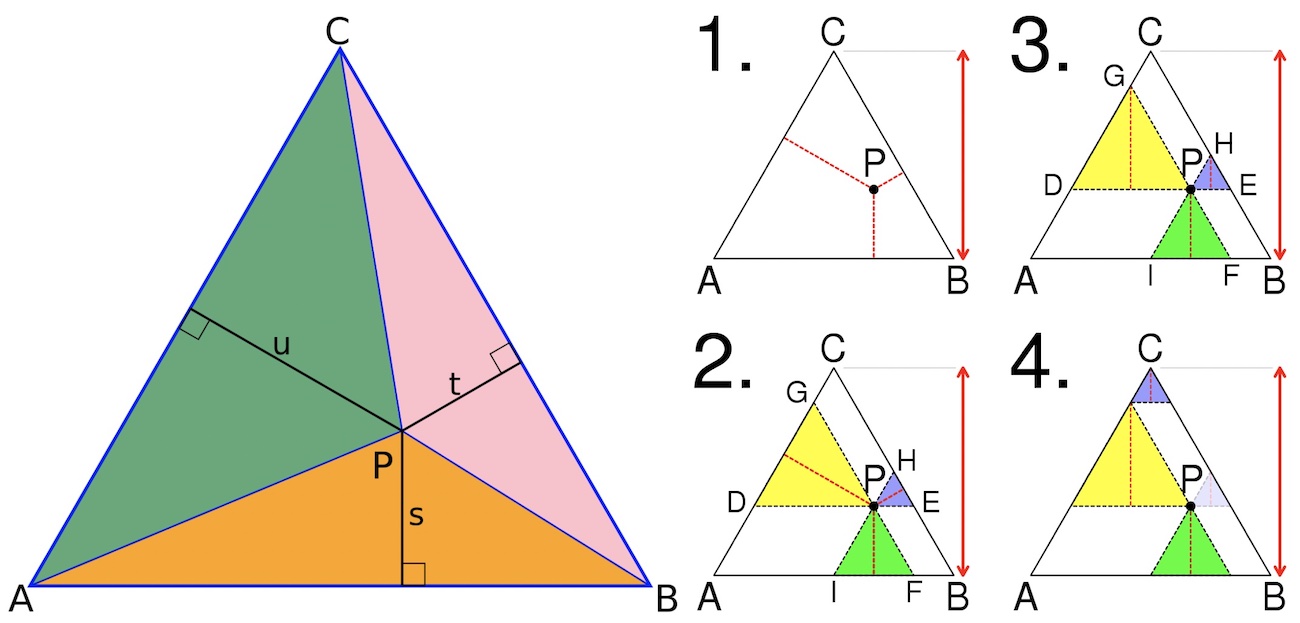
Viviani's theorem states that the sum of the distances from any interior point to the sides of an equilateral triangle equals the length of the triangles's altitude.
First, construct the constraints describing an equilateral triangle centered on the origin, with the distance to each vertex equal to 1. For different size equilateral triangles, the results will scale.
boundaryLine[{{x1_, y1_}, {x2_, y2_}}] = (y1 - y2) x + (x2 - x1) y +
x1 y2 - x2 y1;
boundaryLines[pts_List] :=
boundaryLine /@ Partition[pts, 2, 1, {1, 1}]
trilines = boundaryLines[CirclePoints[3]];
Thread[ trilines > = 0] is the region inside the triangle and Thread[ trilines < = 0] is the region outside the triangle
Find the three distances from {x0,y0} to each side of the triangle
dists = MinValue[{Sqrt[(x - x0)^2 + (y - y0)^2],
trilines[[#]] <= 0}, {x, y}] &/@ Range[3];
Calculate the altitude of the triangle
altitude = MaxValue[y, Thread[trilines >= 0], {x, y}] -
MinValue[y, Thread[trilines >= 0], {x, y}]
3/2
(* find the sum of the three distances *)
sumDists = Total[dists[[All, 1, 1, 1]]];
(* construct the constraints for {x0,y0} to be inside the triangle *)
trix0y0 = Thread[(trilines /. {x -> x0, y -> y0}) >= 0];
(* use Reduce to find the total of the three distances inside the triangle *)
Reduce[res == sumDists && Sequence @@ trix0y0, {res, x0, y0}, Reals]
res == 3/2 && ((x0 == -(Sqrt[3]/2) &&
y0 == -(1/2)) || (-(Sqrt[3]/2) < x0 <= 0 && -(1/2) <= y0 <= (
Sqrt[3] + 3 x0)/Sqrt[3]) || (0 < x0 < Sqrt[3]/2 && -(1/2) <=
y0 <= (Sqrt[3] - 3 x0)/Sqrt[3]) || (x0 == Sqrt[3]/2 &&
y0 == -(1/2)))
Both altitude and the sum of the distances equal 3/2.