I'm trying to model the heat teansfer of an object with cross sectional shape of a 25mm by 25mm square. The top and bottom surface are insulated, so only the side dessipates heat convectively. In the Mathematica code I first tried non-dimensionalize the 2D heat equation but with the time variable unchanged, and then I also tried non-dimensionalize the time variable. These two approach gives me different modeling results, can someone help me take a look of my code and give me some insight? Really appreciated! The two governing equations I used are listed here for reference:
with dimensional time variable: D[θ[t, ξ, ψ], t] - αmodified*(D[θ[t, ξ, ψ], {ξ, 2}] + D[θ[t, ξ, ψ], {ψ, 2}]) dimensionless time variable: D[θ[tau, ξ, ψ], tau] -(D[θ[tau, ξ, ψ], {ξ, 2}] + D[θ[tau, ξ, ψ], {ψ, 2}])
the dimensionless temperature θ=(T-T∞)/(T0-T∞), dimensionless width=x/L, L is the side length of object, equals 25mm, same for dimensionless length ψ=y/L
To make the problem more clear, here's two image, modeled at position ξ = 0.85, ψ = 0.85, the temperature curve from the model with/without dimensionless time looks significantly different although it's all plotted for the real time 0 to 20 sec.
with dimensional time 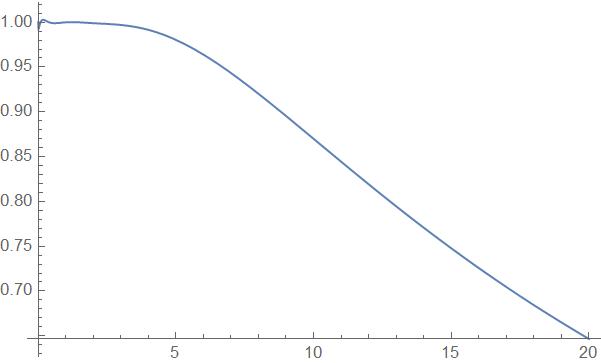
with dimensionless time 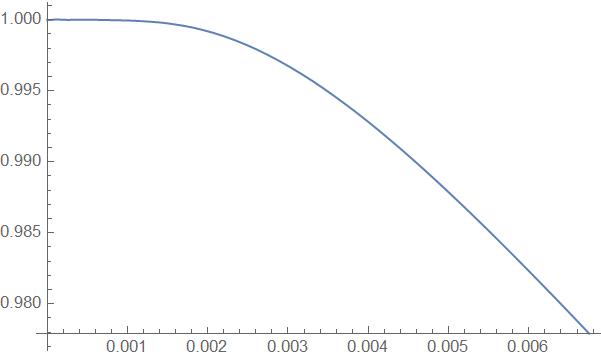
you can tell the temperature evolution is very very different, which in theory they shouldn't
 Attachments:
Attachments: