Hi everyone,
i am trying to create a nice plot of a function in 3d, that consists of three parts: a top part (z>=0), a bottom part (z<0, scaled) and a zero-level plane z=0. However, when using the following code the parametric mesh lines of the lover plot bleed through the plane at z=0 although i explicitly define the PlotRegion only to draw true negative parts:
A = -100 + (5 dt)/(
11 alpha^2 (alpha - Surd[alpha^3 - (1387 dt)/106480, 3]))
Show[Plot3D[A, {alpha, 0.5, 2}, {dt, 0, 10}, RegionFunction -> Function[{alpha, dt, z}, A >= 0], MaxRecursion -> 3, PlotPoints -> 100],
Plot3D[(A/10), {alpha, 0.5, 2}, {dt, 0, 10}, RegionFunction -> Function[{alpha, dt, z}, A < 0], MaxRecursion -> 3, PlotPoints -> 100],
Plot3D[0, {alpha, 0.5, 2}, {dt, 0, 10}, Mesh -> None, PlotStyle -> {Opacity[0.8]}],
{PlotRange -> {Automatic, Automatic, {-6, 5}}}]
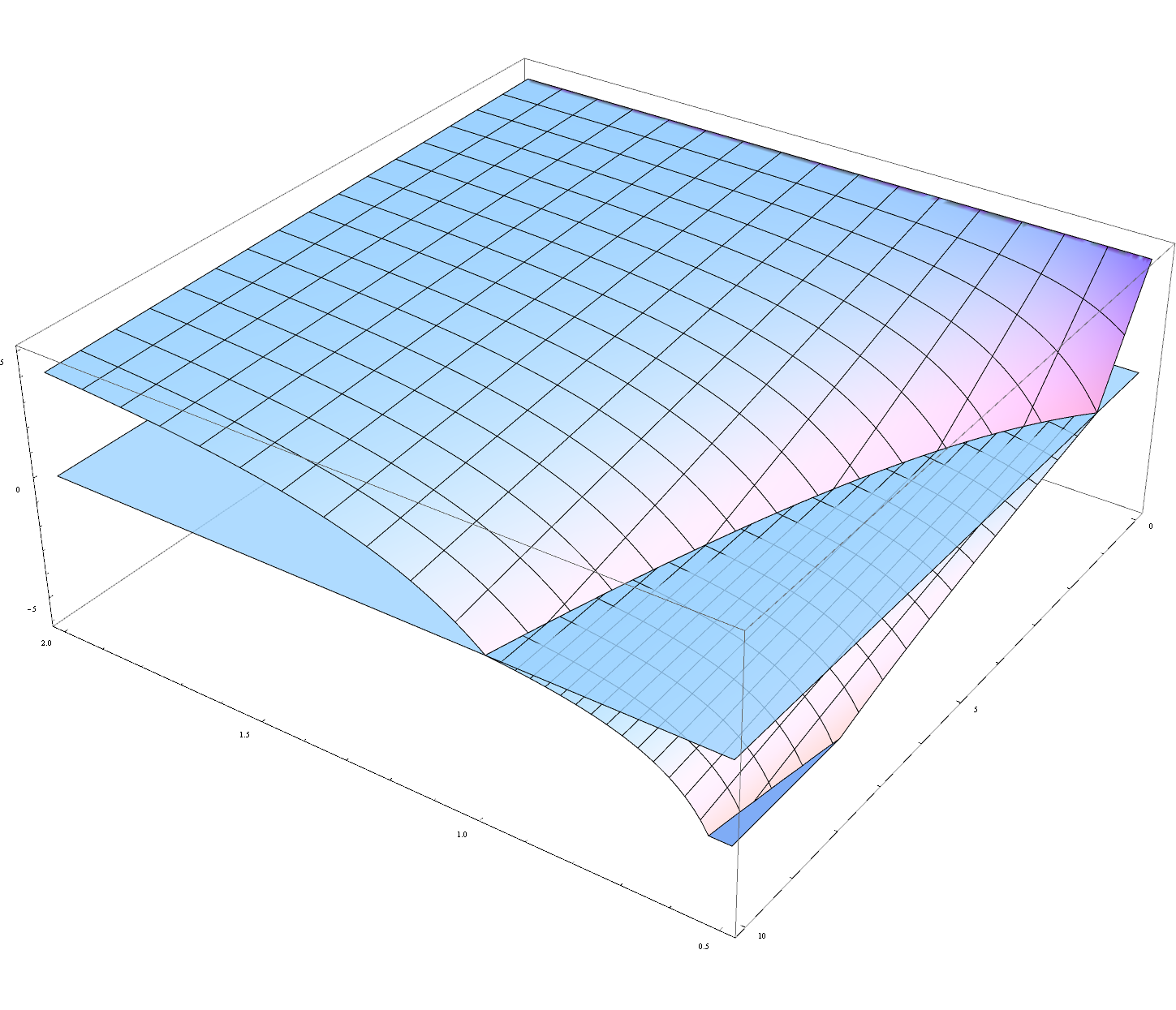
I have read in the docs that mathematica uses depth buffering when everything drawn is opaque and BSP-Trees if transparency is involved. However, despite using transparency the amount of bleeding seems to be view dependent, which should only be the case when using depthbuffer... (also, as you can see only mesh lines behave incorrectly; filled faces are ok). Not using transparency gives the same result.
Any ideas how to prevent this Mesh-bleeding whilest not deactivating the mesh?
Thanks,
Thomas