I have the following dataset:
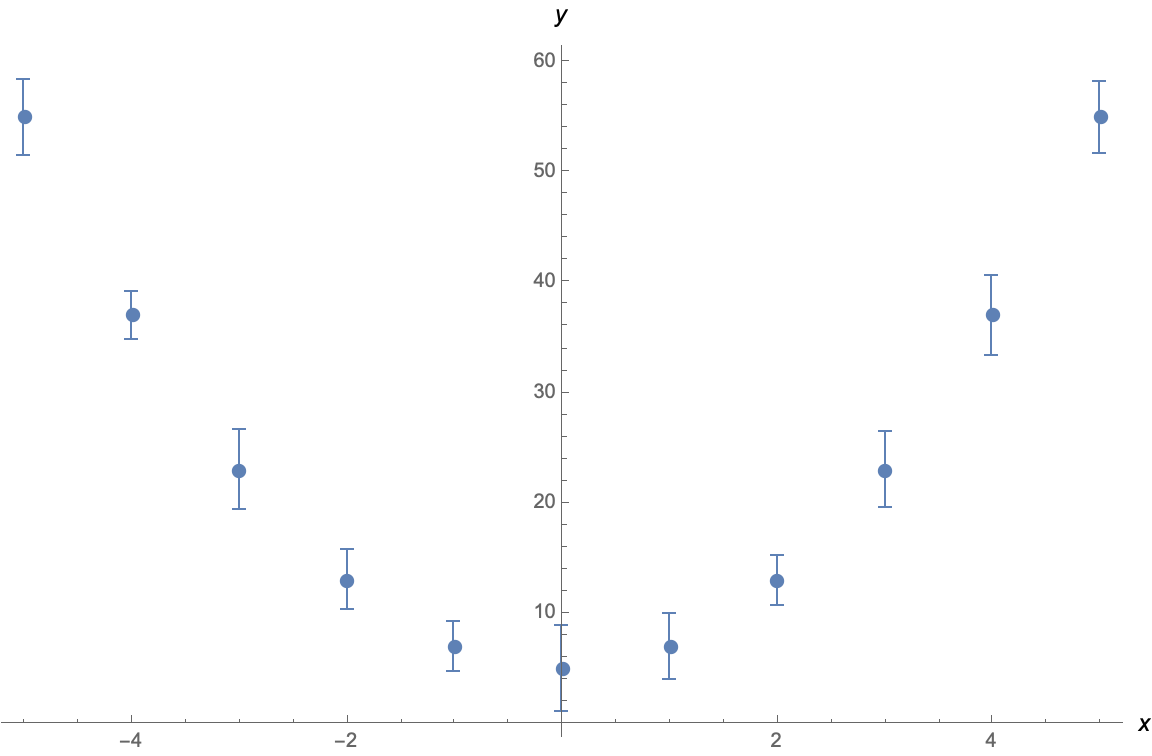
which is generated by data:
data={
{-5, Around[55., 3.42]},
{-4, Around[37., 2.13]},
{-3, Around[23., 3.60]},
{-2, Around[13., 2.69]},
{-1, Around[7., 2.30]},
{0, Around[5., 3.87]},
{1, Around[7., 2.94]},
{2, Around[13., 2.29]},
{3, Around[23., 3.48]},
{4, Around[37., 3.70]},
{5, Around[55., 3.25]}
}
This is actually the plot of
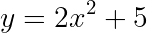
plus some random error.
Now I want to find a fit for this dataset. How do I take into consideration the uncertainty of the measurements? I didn't understand it from the documentation.
NonlinearModelFit[Thread[{data[[All, 1]], data[[All, 2]]}],
a x^2 + b, {a, b}, x, VarianceEstimatorFunction -> (1 &),
Weights -> Map[#[[2]]["Uncertainty"] &, data]]
I should break down this code block for you:
Thread[{data[[All, 1]], data[[All, 2]]}] makes a list of {{x1,y1},{x2,y2},...}
ax2+b is the model to fit
VarianceEstimatorFunction -> (1 &), Weights -> Map[#[[2]]["Uncertainty"] &, data] This is an option I add to NonlinearModelFit that according to the documentation
Using [the above] ∆yi is treated as the known uncertainty of measurement Subscript[y, i], and parameter standard errors are effectively computed only from the weights.
Map[#[[2]]["Uncertainty"] &, data] returns a list of the uncertainties for the points yi's.
But the result I get for this line of code is "too good":
(* FittedModel[5. + 2. x^2 ] *)
What is wrong? Were the uncertainties considered at all?