Luc,
if it is just for the coloring here is a simple and straightforward way. The code should be self-explanatory.
(* your calculated region: *)
reg =
RegionDifference[
RegionIntersection[
BoundaryDiscretizeGraphics[Cuboid[-{.5, .5, .5}, {.5, .5, .5}]],
BoundaryDiscretizeGraphics[Ball[{0, 0, 0}, .65],
MaxCellMeasure -> 0.0005]],
RegionUnion[
BoundaryDiscretizeGraphics[Cylinder[{{0, 0, -.8}, {0, 0, .8}}, .3],
MaxCellMeasure -> 0.0005],
Region[TransformedRegion[
BoundaryDiscretizeGraphics[
Cylinder[{{0, 0, -.8}, {0, 0, .8}}, .3],
MaxCellMeasure -> 0.0005], RotationTransform[Pi/2, {0, 1, 0}]]],
TransformedRegion[
BoundaryDiscretizeGraphics[
Cylinder[{{0, 0, -.8}, {0, 0, .8}}, .3],
MaxCellMeasure -> 0.0005], RotationTransform[Pi/2, {1, 0, 0}]]]]
(* make it a BoundaryMeshRegion: *)
breg = BoundaryDiscretizeRegion[reg];
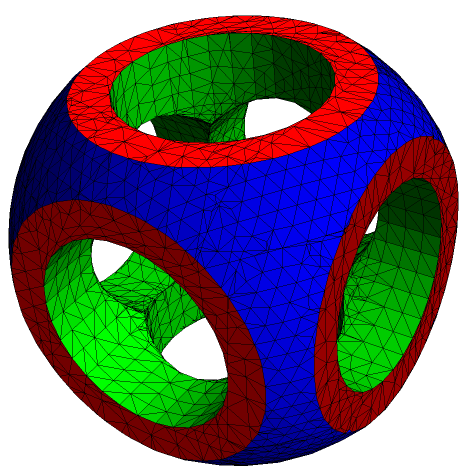
(* calculate all polygons: *)
polygs = MeshPrimitives[breg, 2];
(* selection of polygons according to coordinates (maximal values or on a sphere): *)
redPolygs = Select[polygs, Total[Max /@ Abs @@ #] == 1.5 &];
bluePolygs = Select[polygs, Total[Norm /@ First[#]] > 1.94 &];
greenPolygs = Complement[polygs, redPolygs, bluePolygs];
Graphics3D[{Red, redPolygs, Blue, bluePolygs, Green, greenPolygs}, Boxed -> False]
Addendum: I could not resist playing around a little bit:
(* your outer graphics: *)
gout = Graphics3D[{Red, Cuboid[-{.5, .5, .5}, {.5, .5, .5}], Blue,
Sphere[{0, 0, 0}, .65],
Green, {#,
GeometricTransformation[#, RotationMatrix[Pi/2, {0, 1, 0}]],
GeometricTransformation[#, RotationMatrix[Pi/2, {1, 0, 0}]]} &[
Cylinder[{{0, 0, -.8}, {0, 0, .8}}, .3]]}, Boxed -> False];
(* my "inner" graphics from above: *)
gin = Graphics3D[{Red, redPolygs, Blue, bluePolygs, Green, greenPolygs}, Boxed -> False];
gouto[op_] := (gout /. Graphics3D[p__] :> Graphics3D[{Opacity[op], p}])
gino[op_] := (gin /. Graphics3D[p__] :> Graphics3D[{Opacity[op], p}])
frames = Table[Show[gouto[1 - op], gino[op], Boxed -> False], {op, 0, 1, .05}];
Export["reg.gif", Join[frames, Reverse[frames]]]

Nice things you are doing! Regards -- Henrik