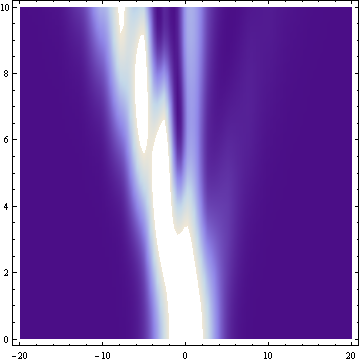
I'm not a physicist, but Numerov's method is used to finding stationary solutions (time-independent Schrodinger equation). When you say scattering and give a potential with that shape it makes me think you want to see how a wave packet is dynamically affected (time-dependent Schrodinger equation). The documentation for NDSolve gives some examples. Here you can see how your potential pushes a wave packet to the left.
NDSolve[{I D[u[t, x], t] + D[u[t, x], x, x] ==
1/(1 + Exp[-x]) u[t, x],
u[0, x] == PDF[NormalDistribution[0, 3], x],
u[t, -100] == u[t, 100]}, u, {t, 0, 10}, {x, -100, 100}]
DensityPlot[Abs[%[[1, 1, 2]][t, x]]^2, {x, -20, 20}, {t, 0, 10},
PlotPoints -> 100]