Dear Wolfram Community:
I wish to share a code I made to do some operations with multidimensional arrays, like tensor products, inner products and inverses/pseudoinverses.
Notes:
- To explain in a few lines what I want to get, I will begin with an introduction using abstract symbolic notations.
- I would greatly appreciate your feedback to this post, because while my code works fine for simple (small) arrays, it become slow for bigger ones and I suspect this could be a clue that my code is not an efficient one: maybe there is a simpler way to do the same.
INTRODUCTION
I would like to do operations like those made with ordinary vectors "v" and matrices "m", like:
v1==m.v2; x=PseudoInverse[m]; x.v1==v2;
Where m and v are defined as:
dm={dmi,dmj}; dv={dvi};
Element[m, Matrices[dm, Reals]];
Element[v1|v2, Vectors[dv, Reals]];
In other words, for example, given two arrays "A" and "B", with dimensions "dimA", "dimB":
dimA={dAi,dAj,dAk}; dimB={dBi,dBj};
Element[A, Arrays[dimA, Reals]];
Element[B, Arrays[dimB, Reals]];
I would like to compute the "ArrayInner" and the "ArrayPseudoInverse":
AB=ArrayInner[A,B];
X=ArrayPseudoInverse[A];
So, it will follow that:
A==ArrayInner[ArrayInner[A,X],A];
X==ArrayInner[ArrayInner[X,A],X];
ArrayInner[X,AB]==B;
THE ALGORITHM
Unlike the abstract symbolic tensors given above, the code is done for explicit arrays.
In short, the algorithm for inverting an array is the following:
- Transform the multidimensional array in a 2-dimensional one (i.e. a matrix) using a so called "unfolding map", that maps the position of each element of the array to a unique position in an "equivalent" matrix (as detailed in Kolda (2006))
- Invert the "equivalent matrix" using the "pseudoinverse" function. I am using the pseudoinverse because usually this equivalent matrix is a singular and rectangular matrix.
- Map the inverted matrix into the respective "inverted array". This was the most difficult part, since inverting the array implies some (sometimes unknown) permutation.
Unfortunately, the full code is very lenghty, so for now I will not copy it in the main text (but I will attach it as a notebook at the end of the post).
EXAMPLE
As an example, I will post the result of inverting an order-3 {I,J,K} array, given in explicit form in the following figure:
1) array A

2) "unfolded array" uA
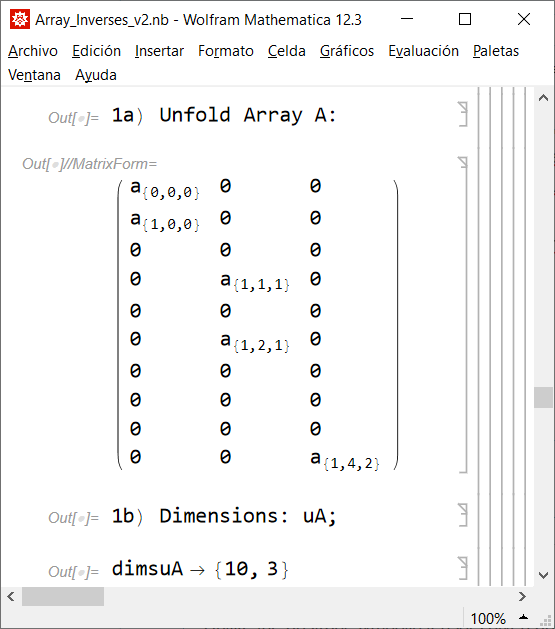
3) "unfolded pseudoinverse" uX
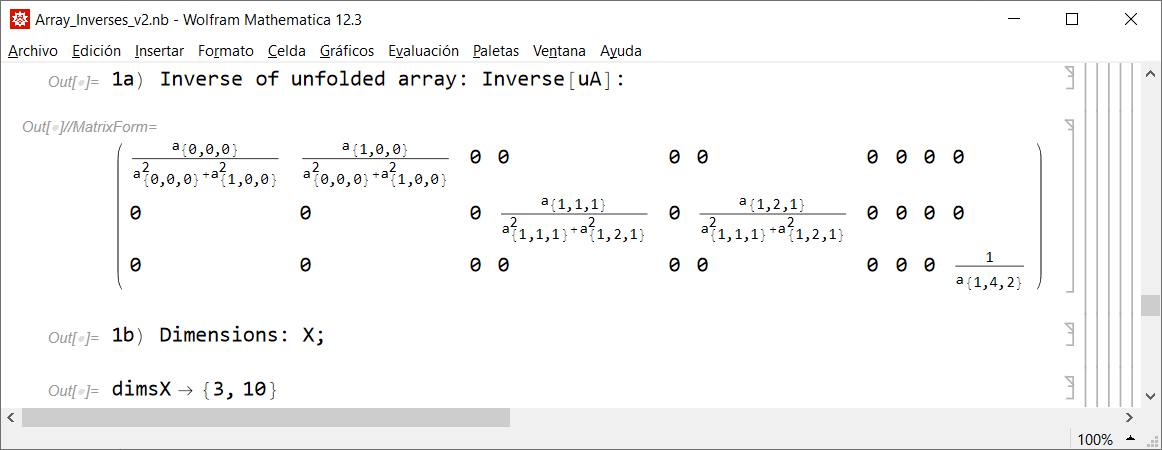
4) inverted array X

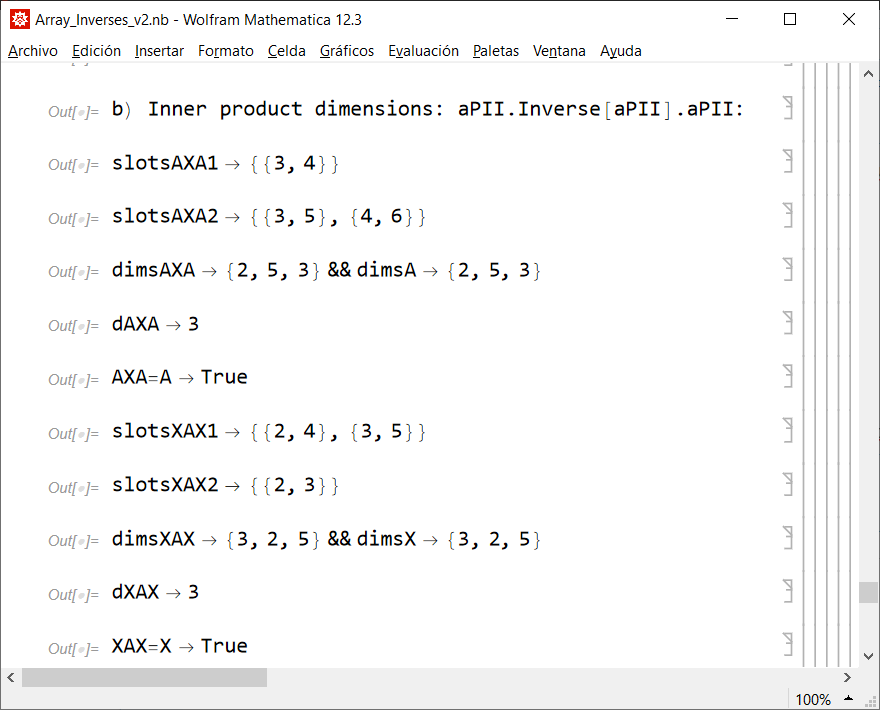
5) Tests to be sure the result is a true inverse: A.X.A==A; X.A.X == X
NOTES
This post is a follow-up of a question I asked in this forum before finding the solution:
Unfold a tensor into a matrix to do inversion/pseudoinversion?
I am very grateful for the support from user Hans Dolhaine, who showed me very useful tips (like how to use the functions "Module" and the solution to a similar problem done with (square) matrices of (square) matrices.
REFERENCES
*) Tamara G. Kolda (2006); "Multilinear operators for higher-order decompositions "; SANDIA REPORT SAND2006-2081
*) Mao-lin Liang, Bing Zheng & Rui-juan Zhao (2018): Tensor inversion and its application to the tensor equations with Einstein product, Linear and Multilinear Algebra
 Attachments:
Attachments: