See if the following helps:
Clear[lappingMeanShuffles, gatherlappingShuffles, lappingShuffles, shuffleInterval, myxIntegers, myyIntegers];
myxIntegers = {11, 28, 66, 36, 94, 8, 44};
myyIntegers = {41, 13, 82, 26, 43, 74, 46};
shuffleInterval[x_List, n_] := Module[{}, Map[({Interval[{# - n, # + n}], #}) &, x]];
lappingShuffles[x_List, n_] := Module[{z = shuffleInterval[x, n]}, Map[Function[y, Select[z, IntervalMemberQ[#[[1]], y] &]], x]];
gatherlappingShuffles[x_List, n_] := Module[{z = lappingShuffles[x, n]}, Map[(#[[All, 2]]) &, z]];
lappingMeanShuffles[x_List, n_] := Module[{z = gatherlappingShuffles[x, n]}, Map[Floor[Mean[#]] &, z]];
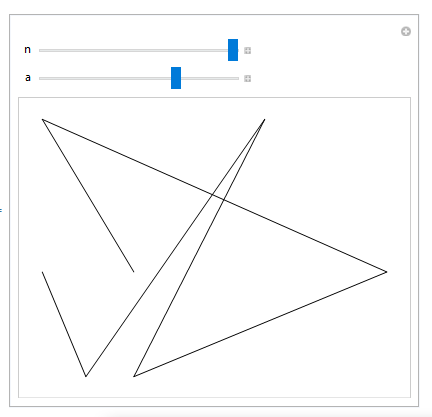
Manipulate[Graphics[Map[Line[#] &, Partition[Transpose[{lappingMeanShuffles[myxIntegers, n], lappingMeanShuffles[myyIntegers, a]}], 2, 1]]], {n, 0, 20, 1}, {a, 0, 20, 1}]
With these parameters (n = 20, a = 14) and the myx..., myy... points we get the resulting image.
If you don't wish to deal with Interval :
(* shuffleInterval[x_List, n_] := Module[{}, Map[({{# - n, # + n}, #})&, x] ];
lappingShuffles[x_List, n_] := Module[{z = shuffleInterval[x, n]}, Map[Function[y, Select[z, Between[y ,#[[1]] ]&] ], x]]; *)
The functions were broken up to make it easier to follow the code but it can be written back into just one function:
concatShuffle[x_List, n_] :=
Module[{},
Map[Floor[Mean[#]] &,
Map[(#[[All, 2]]) &,
Map[Function[y,
Select[Map[({Interval[{# - n, # + n}], #}) &, x],
IntervalMemberQ[#[[1]], y] &]], x]] ] ];
concatShuffle[{11, 28, 66, 36, 94, 8, 44}, 10]
(* {9, 32, 66, 36, 94, 9, 40} *)
`
Thanks