While radioactivity was discovered around turn of century 1900, the technique of dating by Carbon-14 decay was not formulated until half a century later. Somewhere in between, around 1921, Polya became interested in lattice walks (and see references therein). Sufficiently simple lattice walks have simple, countable multiway graphs.

For example, Polya's original experiment allows a pawn to move on a regular grid by $\pm(0,1)$ or $\pm(1,0)$ at each time interval, and asks how many even-length paths return to the origin after time $2t$. Amazingly, the answer turns out to have to do with the expansion coefficients of the complete elliptic integral of the first kind (and we can prove this using Creative Telescoping). To just get a sense of what happens, let's calculate the first few terms:

moves = Join[IdentityMatrix[2], -IdentityMatrix[2]];
AXIOM = {{Branch[{0, 0}]}, {Branch[{0, 0}]}};
Iterate[state_] := With[{nextState = Flatten[
     Outer[Append[#1, #1[[-1]] + #2] &, state[[1]], moves, 1], 1]},
  {Complement[nextState, #], Join[state[[2]], #]} &@
   Select[nextState, #[[-1]] == {0, 0} &]]
data = NestList[Iterate, AXIOM, 10];
Differences@Partition[Length /@ data[[All, 2]], 2][[All, 1]]
%/4

Out[]={4, 20, 176, 1876}
Out[]={1, 5, 44, 469}

We can look the sequence up on OEIS, its number is A054474. This sequence is related to the expansion of EllipticK:

CoefficientList[Series[2/Pi EllipticK[16 x], {x, 0, 4}], x]
{1, 4, 36, 400, 4900}

To see exactly how, let's look at the multiway graph

Graphics3D[{Arrowheads[0.02],
  data[[5]] /. Branch[x__] :> Arrow /@ Partition[
      MapIndexed[{Sequence @@ #1, -#2[[1]]} &, {x}], 2, 1]
  }, ImageSize -> 500, Boxed -> False]

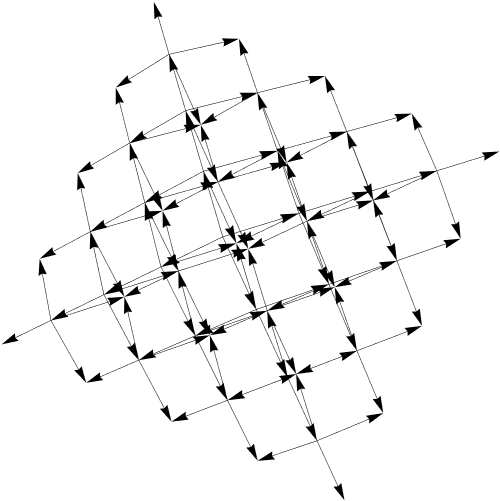
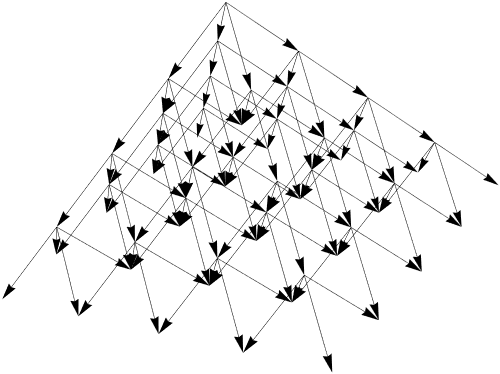
Notice that the central axis is terminal for vectors, except at the top of the pyramid. This is by design, since the iterator selects out paths that return to the origin, and ceases building on them. If we want to allow paths to visit the origin multiple times, we already have all the data we need. For example:

SameQ[20 + 4^2, 36]
SameQ[176 + 4^3 + 20*4*2, 400]
Out[]= True,True

If you understand combinatorics terms like $4^2$, $4^3$, and $20*4*2$ have to do with splicing together paths of shorter length. There is a regular way to extend these sorts of calculations to infinity, maybe using something like Bell polynomials, but we aren't too concerned here.

Notice that there is always an extra factor of $4$, which indicates hidden cyclic or dihedral symmetry. We can make symmetry more obvious through animation of the origin-returning walks (using the previous chess assets). Here we plot four walks:

data[[3, 2, 2 ;; -1]]
Out[]={
 Branch[{0, 0}, {-1, 0}, {0, 0}], Branch[{0, 0}, {0, -1}, {0, 0}], 
 Branch[{0, 0}, {0, 1}, {0, 0}], Branch[{0, 0}, {1, 0}, {0, 0}]}
WorldChessPawnDancers@% 

This is not very interesting, but if we step up to the $20$ walks of length $t=4$, we can barely cram them onto a regulation chess board (with four extra pawns at no cost). There is some artistry involved in how to synchronize movements so that pawns can move pairwise and change partners, as we did in the good old days square dancing in Arkansas, ha ha ha. What I came up with yesterday might not be the best choreography, can anyone do better? And does anyone have a six-step choreography for a grand ball of 176 pawns moving in synchrony? How big must we make the game board?