Mainly change {r, 0.01, 3, 0.001} to {r, 1/100, 3, 1/1000} to reduce round-off error. Also, if just producing the plot is the objective and not a table of results, then {r, 1/100, 301/100, 1/100} is more than adequate and much faster.

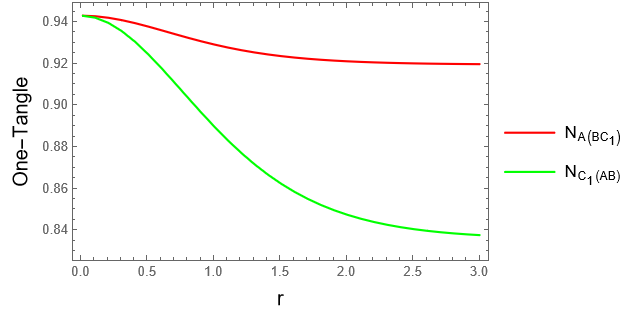
NeABC = Table[{r, 2 N[Sum[(Sqrt[3 + 2 n + Cosh[2 r]] Sech[r]^2 Tanh[r]^(2 n))/(3 Sqrt[1 + Cosh[2 r]]),
  {n, 0, \[Infinity]}]]}, {r, 1/100, 301/100, 1/10}];
NeCAB = Table[{r, 2 N[Sum[(2 Sqrt[1 + n] Sech[r]^2 Tanh[r]^(2 n))/(3 Sqrt[1 + Cosh[2 r]]),
  {n, 0, \[Infinity]}]]}, {r, 1/100, 301/100, 1/10}];

ListLinePlot[{NeABC, NeCAB}, DataRange -> {0, 3}, FrameLabel -> {Style["r", 15, Black], 
   Style["One-Tangle", 15, Black]}, Frame -> True,  RotateLabel -> True, 
   PlotStyle -> {{Dashing[Block], Red}, {Dashing[Block], Green}}, 
   PlotLegends -> {Text["\!\(\*SubscriptBox[\(N\), \(A \((\*SubscriptBox[\(BC\), \(1\)])\)\)]\)"], 
   Text["\!\(\*SubscriptBox[\(N\), \(\*SubscriptBox[\(C\), \(1\)] \((AB)\)\)]\)"]}]