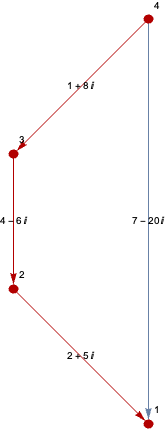
Henrick,

One way would be to construct another graph with each weight replaced by its Abs value.

g1 =
  Graph[{2 \[DirectedEdge] 1, 3 \[DirectedEdge] 2, 
    4 \[DirectedEdge] 3, 4 \[DirectedEdge] 1},
   EdgeWeight -> {2 \[DirectedEdge] 1 -> 2 + 5 I, 
     3 \[DirectedEdge] 2 -> 4 - 6 I, 4 \[DirectedEdge] 3 -> 1 + 8 I, 
     4 \[DirectedEdge] 1 -> 7 - 20 I},
   VertexLabels -> "Name",
   EdgeLabels -> "EdgeWeight"];

realWeights = PropertyValue[g1, EdgeWeight] // Abs;
g2 = Graph[g1, EdgeWeight -> realWeights];
shortestPath = FindShortestPath[g2, 4, 1];

HighlightGraph[g1, PathGraph[shortestPath, DirectedEdges -> True]]