Please help me to achieve the 3 x 3 from the steps I undertook. I did line1 since ad A1 (2 x 2 matrix). I attempted to equate line 2, hoping to get line 3 (output which is 3 x 3 matrix). I attempted to equate line 2, hoping to get line 3 (output which is 3 x 3 matrix). I added the 'commented out' part of the code which I suspect it is a direction in moving from a 2x2 to 3x3 matrix, it's just that I don't have the right Mathematica syntax. See attachment. 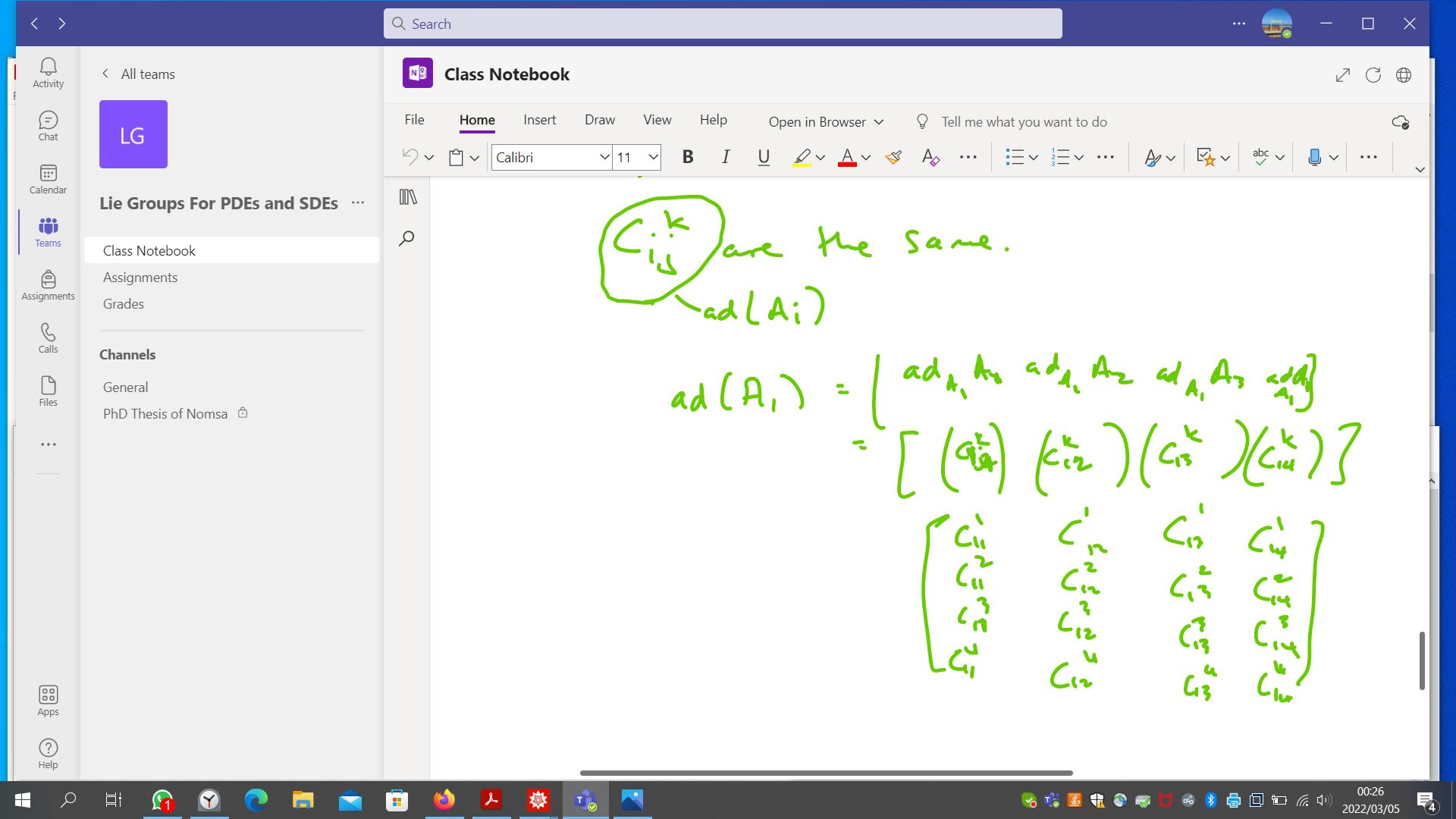
(*_____ This is how one enters the input : {A1={{1,0},{0,-1}}, \
A2={{0,1},{0,0}}, A3={{0,0},{1,0}}} __________*)
(*_____ Note that the order in which one inputs matters _______*)
newlistSym = Input["Please input a basis in a list form"];
dim = Length[newlistSym];
AdjointMatrixCommutator[A1, A3] = Dot[A1, A3] - Dot[A3, A1]
(* adA3 = AdjointMatrixCommutator[A1,A3] == Table[c[1, 3, k], {k, 1, \
dim}]*)
AdjointMatrixCommutator[A1, A2] = Dot[A1, A2] - Dot[A2, A1]
(*ad A2 = AdjointMatrixCommutator[A1,A2] == c[1, 2, k], {k, 1, dim}*)
AdjointMatrixCommutator[A1, A1] = Dot[A1, A1] - Dot[A1, A1]
(*ad A1 = AdjointMatrixCommutator[A1,A3] == c[1, 1, k], {k, 1, dim}*)
 Attachments:
Attachments: