Message Boards Message Boards

GROUPS:
Mathematica Wolfram Language Numerical Computation
xslittlegrass *

How to simulate a low precision calculation?

xslittlegrass *
Posted 9 years ago
6798 Views
|
4 Replies
|
6 Total Likes
|
I recently encountered some unexpected behavior in my numerical simulation, and I suspect that may come from the round off error in the calculation. I plan to test it using low precision calculations, but I can't figure out how to do that.

For example, a Fourier transform
f[x_] = Cos[2 \[Pi] x];
N0 = 10;
ls = Most@Array[f, N0, {0, 1}];

using the default machine precision I get

Fourier[ls]

{-6.4763*10^-17 + 0. I, 1.5 + 5.55112*10^-17 I, 1.60247*10^-17 + 2.77556*10^-17 I, 3.23815*10^-17 - 8.01234*10^-18 I, -1.60247*10^-17 - 2.77556*10^-17 I, -1.60247*10^-17 + 2.77556*10^-17 I, 3.23815*10^-17 + 8.01234*10^-18 I, 1.60247*10^-17 - 2.77556*10^-17 I,1.5 - 5.55112*10^-17 I}

but using fixed lower precision, I get

Block[{$MaxPrecision = 8, $MinPrecision = 8},
Fourier[SetPrecision[ls, 8]]]

{-4.3981121*10^-35, 1.5000000, 1.8230938*10^-34, 2.1989581*10^-35, 1.8230938*10^-34, 1.8230938*10^-34, 2.1989581*10^-35, 1.8230938*10^-34, 1.5000000}

It appears that fix 8 precision has smaller errors than the default machine precision. I would expect using fixed precision at 8 would give larger errors than machine precision. So why does it behave like this, and what are the correct ways to simulate the low precision calculations?
POSTED BY: xslittlegrass *
4 Replies
Sort By:
The result is decidedly not of high precision. If you check the InputForm you will see it is 8 as expected. What it is, however, is high accuracy on the zeros.

{-4.404185501080837196522866226126013806214324`8.*^-35,
 1.49999999999999999999999999999999982511`8.,
 1.8253664026743891567492525318255642007953505`8.*^-34,
 2.202092750540418598261433113063006903107162`8.*^-35,
 1.8251704869492521088312577424026938265157147`8.*^-34,
 1.8251704869492521088312577424026938265157147`8.*^-34,
 2.202092750540418598261433113063006903107162`8.*^-35,
 1.8253664026743891567492525318255642007953505`8.*^-34,
 1.49999999999999999999999999999999982511`8.}

So we know these are zero to 35 or so places (to the extent that working in fixed precision does not mess things up), but we do not know the actual digit values at all well.
POSTED BY: Daniel Lichtblau
It appears that fix 8 precision has smaller errors than the default machine precision. I would expect using fixed precision at 8 would give larger errors than machine precision. So why does it behave like this
As mentioned on ref/Precision, machine precision is considered lower than any explicit precision like 8. The machine precision computation is carried out directly using the computer's native floating point arithmetic, hence without any error tracking. This has the advantage of being very fast. On the other hand, when using precision 8, the arbitrary-precision routines are used instead and the error is tracked to keep the result is as accurate as possible given the input precision and operations performed.
POSTED BY: Ilian Gachevski
Thanks for the answers. I tried to make the example in Sean's answer into a fortran (at the end), and by compile with
ifort test.f90or ifort -r8 test.f90
I can set it to use single (fixed precision at 8) or double precision (fixed precision at 16).And the results are expected, that double precision gives smaller errors.
In Sean's example, it shows that even fixed precision at 1 would give a smaller error compared to machine precision. This seems to suggested that Mathematica uses higher precision in the calculation even we set set $MaxPrecision or $MinPrecision to a small number (for example 1). This is very confusing for me, because I though setting $MinPrecision and $MaxPrecision t0 8 would minic the single precision calculation, and setting $MinPrecision and $MaxPrecision to 16 would minic the double precision calculation. So could you explain the differences between a calculation by setting setting $MinPrecision and $MaxPrecision to 16 and a machine precision calculation? And is there ways to minic the round off error in low precision calculations?
----------------------
test program 
program main
implicit none
real :: Pi=4.0*atan(1.0)
integer,parameter :: n=9
integer r,s
real :: x(n)
complex :: ft(n)
complex :: ci=(0.,1.)
do r=1,n
  x(r)=cos(2.*(r-1.)*Pi/n)
end do
do s=1,n
  ft(s)=(0.,0.)
  do r=1,n
   ft(s) = ft(s)+ x(r)*exp(2.*Pi*ci*(r - 1.)*(s - 1.)/n)
  end do
  ft(s)=ft(s)/sqrt(real(n))
end do
do r=1,n
  write (*,*) ft(r)
end do
end program


single precision, compiled with
ifort test.f90
results:
(1.9868216E-08,0.0000000E+00)
(1.500000,3.2782555E-07)
(2.5828680E-07,-4.1723251E-07)
(7.9472862E-08,-1.7881393E-07)
(1.1920929E-07,-1.7881393E-07)
(1.3907750E-07,-4.5696893E-07)
(-4.5696893E-07,-2.5828680E-07)
(-6.7551929E-07,-1.3907750E-07)
(1.500000,1.5695890E-06)

double precision, compiled with
ifort -r8 test.f90
results:
(-2.960594732333751E-016,0.000000000000000E+000)
(1.50000000000000,2.220446049250313E-016)
(-1.850371707708594E-017,-1.110223024625157E-016)
(-1.665334536937735E-016,-3.700743415417188E-017)
(1.850371707708594E-016,1.295260195396016E-016)
(-6.661338147750939E-016,-3.515706244646329E-016)
(4.625929269271486E-016,-7.401486830834377E-017)
(4.903485025427775E-016,7.771561172376096E-016)
(1.50000000000000,-2.090920029710711E-015)
POSTED BY: xslittlegrass *
Let's write our own DFT function for a comparison
I've taken the code for this from the documentation for Fourier. Let's fist compute the values symbolically
(* Calculate the DFT symbolically *)
x = ls; n = Length[x]; u /: Subscript[u, r_] := x[[r]];
FullSimplify[Table[(1/Sqrt[n])*Sum[Subscript[u, r]*E^(2*Pi*I*(r - 1)*((s - 1)/n)), {r, 1, n}], {s, 1, n}]]

{0, 3/2, 0, 0, 0, 0, 0, 0, 3/2}
We can run this same code with different precisions and compare to the "correct" results above.
(*With precision = 8*)
Block[{$MaxPrecision = 8, $MinPrecision = 8},
x = SetPrecision[ls, 8]; n = Length[x]; u /: Subscript[u, r_] := x[[r]];
Table[(1/Sqrt[n])*Sum[Subscript[u, r]*E^(2*Pi*I*(r - 1)*((s - 1)/n)), {r, 1, n}], {s, 1, n}]
]

{-4.4041855*10^-35, 1.5000000, 1.8255231*10^-34, 2.2020928*10^-35,
1.8255231*10^-34, 1.8255231*10^-34, 2.2020928*10^-35, 1.8255231*10^-34, 1.5000000}
(*With boring old machine precision*)
x = N[ls]; n = Length[x]; u /: Subscript[u, r_] := x[[r]];
Table[(1/Sqrt[n])*Sum[Subscript[u, r]*E^(2*Pi*I*(r - 1)*((s - 1)/n)), {r, 1, n}], {s, 1, n}]

{-1.11022*10^-16, 1.5 + 0. I, -9.25186*10^-17 + 0. I,
0. + 0. I, -1.11022*10^-16 + 0. I, -1.11022*10^-16 + 0. I,
0. + 0. I, -9.25186*10^-17 + 0. I, 1.5 + 0. I}


So the built-in compiled version and a version we built in Mathematica do the same thing.  If we run with a bunch of different precisions, we can see how the results differ based on the accuracy of the numbers used (X axis is precision used. Y axis is how off the actual results the calculations end up being. Closer to 0 is better ):

    

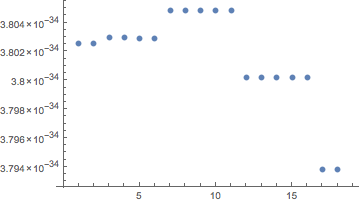
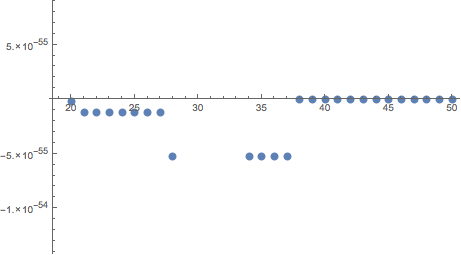
Higher precision is generally good, but answering "Why is not always the case that that is true" can be difficult. After all, if I asked "why does 0.1+0.2 give 0.30000000000000004 in floating point computation?" what answer could be given except to walk step-by-step through how the addition plays out in floating point in all the painful detail?

Higher precision usually means better answers, yes, but there's nothing that guarantees this that I know of.
POSTED BY: Sean Clarke
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract