In order to find the area of the atypical figure, I approached the idea of using Fourier descriptor to find the outskirts, and then using Monte Carlo to find the area of an object. Using Fourier descriptor, we implemented the outer edge of the image below. Using the idea of finding the unstructured area using Monte Carlo, how can we implement the area of the circle below using Monte Carlo? I'm curious about how you can apply it to unstructured shapes, not to the formula to find a circle. Or do you have any other ideas to compare the error with the original image (attached image) of the outer periphery obtained by Fourier descriptor?
original image 
img = Import[""];
img = Binarize[img~ColorConvert~"Grayscale"~ImageResize~500~Blur~3];
pts = DeleteDuplicates@
Cases[Normal@
ListContourPlot[Reverse@ImageData[img],
Contours -> {0.5}], _Line, -1][[1, 1]];
center = Mean@MinMax[pts] & /@ Transpose@pts;
pts = # - center & /@ pts[[;; ;; 20]];
potholePlot = ListPlot[pts, AspectRatio -> Automatic]
![enter image description here][2]
SetAttributes[toPt, Listable]
toPt[z_] := ComplexExpand[{Re@z, Im@z}] // Chop;
cf = Compile[{{z, _Complex, 1}},
Module[{n = Length@z},
1/n*Table[Sum[z[[k]]*Exp[-I*i*k*2 Pi/n], {k, 1, n}], {i, -m, m}]]];
z = pts[[All, 1]] + I*pts[[All, 2]];
m = 50;
cn = cf[z];
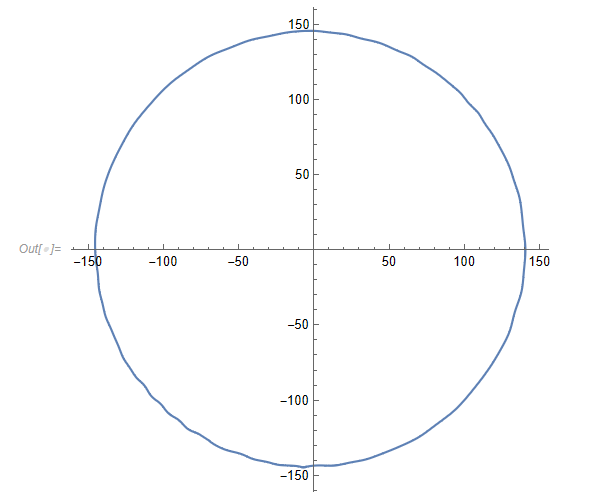
{f[t_], g[t_]} =
Sum[cn[[j]]*Exp[I*(j - m - 1)*t], {j, 1, 2 m + 1}] // toPt;
ParametricPlot[{f[t], g[t]}, {t, 0, 2 Pi}, AspectRatio -> Automatic]