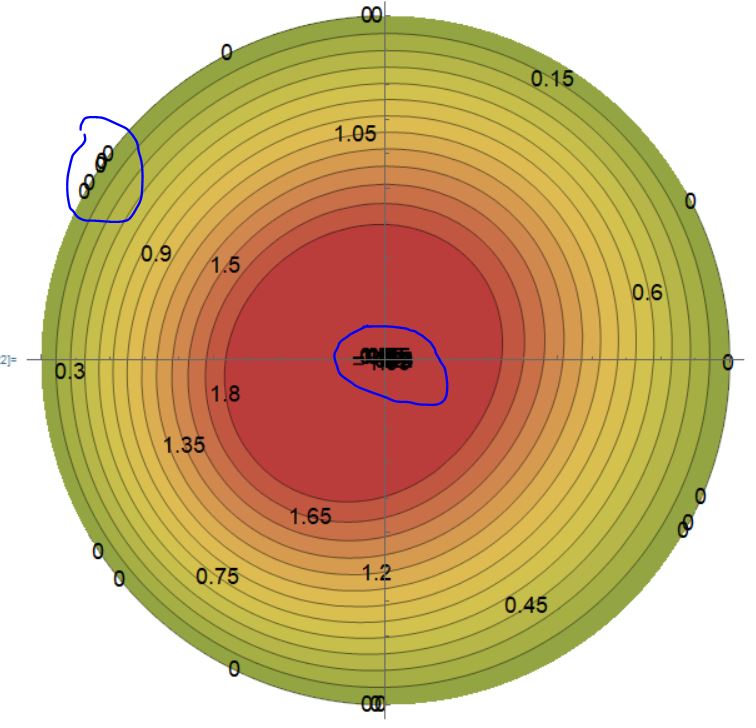
Here is my code. I want to get rid of these repeated contour labels as shown in the Figure above. Please help!!

ClearAll["Gloabal`*"];
    \[Epsilon] = 0.3;
    \[Lambda] = 1;
    \[Eta] = 2.404830;
    Q = 200;
    r0 = 0.000001;
    \[Beta] = ArcSin[\[Lambda]/Sqrt[1 + \[Lambda]^2] ];
    Subscript[T, 0] = (\[Eta] BesselJ[0, \[Eta] r])/(2 BesselJ[1, \[Eta]]);
    eqn = F''[r] + 1/r F'[r] - F[r]/
        r^2 + \[Eta]^2 F[r] == \[Eta]^2 r Subscript[T, 0];
    bcs = {F[1] == 0, F'[r0] == 0};
    sol = Flatten[NDSolve[{eqn, bcs}, F, {r, r0, 1}]];
    fr = Flatten[F[r] /. sol];
    Subscript[Nu, 
      2] = \[Eta]^2/
       4 NIntegrate[((1 - 2 r^2) Subscript[T, 0]^2 + 
           2 r fr Subscript[T, 0]) r, {r, r0, 1}]/
       N[Integrate[Subscript[T, 0]^2 r, {r, 0, 1}]];
    Subscript[T, 1] = fr Sin[\[Zeta]];
    eqn1 = r^2 k''[r] + r k'[r] - 
        4 k[r] + \[Eta]^2 r^2 k[r] == -((\[Eta]^2 fr r^3)/
         2) + (\[Eta]^2 r^4)/2 Subscript[T, 0];
    bcs1 = {k[1] == 0, k'[r0] == 0};
    sol1 = Flatten[NDSolve[{eqn1, bcs1}, k, {r, r0, 1}]];
    kr = Flatten[k[r] /. sol1];
    eqn2 = r^2 l''[r] + 
        r l'[r] + \[Eta]^2 r^2 l[r] == (\[Eta]^2 Subscript[T, 0] r^2)/4 - 
        Subscript[Nu, 2] Subscript[T, 0] r^2 + (\[Eta]^2 fr r^3)/
        2 - (\[Eta]^2 r^4)/2 Subscript[T, 0];
    bcs2 = {l[1] == 0, l'[r0] == 0};
    sol2 = Flatten[NDSolve[{eqn2, bcs2}, l, {r, r0, 1}]];
    lr = Flatten[l[r] /. sol2];
    Subscript[T, 2] = kr Cos[2 \[Zeta]] + lr;
    eqn3 = r^2 H1''[r] + r H1'[r] - H1[r] + \[Eta]^2 r^2 H1[r] == 
       1/4 r^2 fr \[Eta]^2 - 3/4 r^4 fr  \[Eta]^2 - 1/2 r^3 kr \[Eta]^2 + 
        r^3 lr  \[Eta]^2 - r^2 fr  Subscript[Nu, 2] - 
        1/4 r^3 \[Eta]^2 Subscript[T, 0] + 
        3/4 r^5 \[Eta]^2 Subscript[T, 0] + 
        r^3 Subscript[Nu, 2] Subscript[T, 0];
    bcs3 = {H1[1] == 0, H1'[r0] == 0};
    sol3 = Flatten[NDSolve[{eqn3, bcs3}, H1, {r, r0, 1}]];
    Hr1 = Flatten[H1[r] /. sol3];

    eqn4 = r^2 i''[r] + r i'[r] - i[r] + \[Eta]^2 r^2 i[r] == 0;
    bcs4 = {i[1] == 0, i'[r0] == 0};
    sol4 = Flatten[NDSolve[{eqn4, bcs4}, i, {r, r0, 1}]];
    ir = Flatten[i[r] /. sol4];
    eqn5 = r^2 j''[r] + r  j'[r] - 4 j[r] + \[Eta]^2 r^2 j[r] == -1/
        6 Q r^4 \[Lambda] Cos[\[Beta]] \[Eta]^2 Subscript[T, 0];
    bcs5 = {j[1] == 0, j'[r0] == 0};
    sol5 = Flatten[NDSolve[{eqn5, bcs5}, j, {r, r0, 1}]];
    jr = Flatten[j[r] /. sol5];

    eqn6 = r^2 k1''[r] + r  k1'[r] - 4 k1[r] + \[Eta]^2 r^2 k1[r] == 0;
    bcs6 = {k1[1] == 0, k1'[r0] == 0};
    sol6 = Flatten[NDS{eqn6, bcs6}, k1, {r, r0, 1}]];
    kr1 = Flatten[k1[r] /. sol6];

    eqn7 = r^2 l1''[r] + r  l1'[r] - 9 l1[r] + \[Eta]^2 r^2 l1[r] == 
       1/4 r^4 fr \[Eta]^2 + 1/2 r^3 kr \[Eta]^2 - 
        1/4 r^5 \[Eta]^2 Subscript[T, 0];
    bcs7 = {l1[1] == 0, l1'[r0] == 0};
    sol7 = Flatten[NDSolve[{eqn7, bcs7}, l1, {r, r0, 1}]];
    lr1 = Flatten[l1[r] /. sol7];

    eqn8 = r^2 m''[r] + r  m'[r] - 9 m[r] + \[Eta]^2 r^2 m[r] == 0;
    bcs8 = {m[1] == 0, m'[r0] == 0};
    sol8 = Flatten[NDSolve[{eqn8, bcs8}, m, {r, r0, 1}]];
    mr = Flatten[m[r] /. sol8];

    eqn9 = r^2 n''[r] + r  n'[r] - 9 n[r] + \[Eta]^2 r^2 n[r] == 0;
    bcs9 = {n[1] == 0, n'[r0] == 0};
    sol9 = Flatten[NDSolve[{eqn9, bcs9}, n, {r, r0, 1}]];
    nr = Flatten[n[r] /. sol9];
    Subscript[T, 3] = 
      Hr1 Sin[\[Zeta]] + ir Cos[\[Zeta]] + jr Sin[2 \[Zeta]] + 
       kr1 Cos[2 \[Zeta]] + lr1 Sin[3 \[Zeta]] + mr Cos[3 \[Zeta]] + nr;
    Tsum = Subscript[T, 
       0] + \[Epsilon] Subscript[T, 1] + \[Epsilon]^2 Subscript[T, 
        2] + \[Epsilon]^3 Subscript[T, 3];
    plot = ContourPlot[
       Tsum /. {r -> Norm[{x, y}], \[Zeta] -> ArcTan[y, x]}, {x, -1, 
        1}, {y, -1, 1},
       ColorFunction -> "DarkRainbow",
       RegionFunction -> (Norm[{#, #2}] <= 1 &),
       Frame -> False,
       Axes -> True,
       TicksStyle -> Directive[FontOpacity -> 0],
       Contou-> 30,
       ContourShading -> Automatic,
       ContourLabels -> {Style[Text[#3, {#1, #2}], 18] &, 
         Tooltip[#3, #2, TooltipStyle -> FontSize -> 10] &},
       ImageSize -> Large
       ];

plot