This post will illustrate how to use computer algebra systems (in particular, Mathematica) for solving a security problem in DeFi, that is, the "safe" computation of prices of LP tokens.

This post may interest the following audience:

1. Developers interested in creating new lending protocols that accept LP tokens (that are more complex than Uniswap) as collateral;
2. Mathematica-users (or other CAS-users) that are curious about applications of these tools to DeFi.

Introduction

Automated market makers (AMMs) are smart contracts that helps users to swap between assets without using the traditional approach of order books. First popularized by Uniswap, AMMs are a fundamental piece of decentralized finance (DeFi), and many types of AMMs exist today.

In the literature, AMMs is also known as constant function market makers (CFMMs). The reason for this name comes from their use of an invariant trading function:

"CFMMs use a single rule that determines whether or not a proposed trade is accepted. The rule is based on evaluating a trading function, which depends on the proposed trade and the current reserves of the CFMM. A proposed trade is accepted if the value of the trading function at the post-trade reserves (with a small correction for the trading fee) equals the value at the current reserves, i.e., the function is held constant." - From Angeris, Guillermo, et al. "Constant function market makers: Multi-asset trades via convex optimization." arXiv preprint 2107.12484 (2021).

For example, Uniswap uses the trading function

$ \varphi(r_1,r_2)=r_1r_2 $

while Balancer uses the trading function

$ \varphi(r_1,r_2,\ldots,r_n)=r_1^{w_1} r_2^{w_2}\cdots r_n^{w_n} $

where $r_i$ is the amount of reserves of the i-th token.

(Other examples and more details can be seen in the excellent article from Angeris et. al.)

Pricing of LP tokens

The reserves of CFMMs are created by users interested in gaining a fraction of the trading fee, and in some cases, some bonus assets. In particular, every time liquidity is added to a CFMM, most implementations give the user a liquidity provider (LP) token representing the user's share of the pool.

In the spirit of DeFi composability, lending protocols such as Warp Finance accepts these LP tokens as collateral for borrowing other assets. Thus, it is essential to have a method to price LP tokens in order to know if the collateral should be liquidated or not.

Let LPP denotes the price of the LP token. A naive method for pricing the LP token is given by

$ LPP = \frac{TVL}{TS} =\frac{\sum_{i=1}^{n} r_i p_i}{TS} $

where:

• TVL is the total value locked;
• TS is the total supply of the token;
• $r_i$ is the amount of reserves of the i-th token;
• $p_i$ is the basis price (e.g. in USD) of the i-th token and
• $n$ is the total number of different assets in the pool.

While simple, this pricing method is vulnerable to manipulations: an attacker could use a flash loan to swap a gigantic quantity of tokens and, consequently, manipulate LPP by changing the reserve $r_i$ of one of the assets. For more details you can see the through explanation on Christoph Michel's blog.

To mitigate this attack vector, Alpha Finance introduced the notion of fair Uniswap LP pricing. Briefly, the idea is to use Uniswap invariant K and the prices (which is assumed to come from a secure oracle - an assumption that we can't always assume to be true) to estimate the price of LP token instead of the reserves. Since K isn't changed when the token is swapped and the price comes from an oracle (supposedly secure), it mitigates attacks caused by swapping tokens.

Could this "fairness" be generalized to more complex CFMMs, such as Balancer pools for multiple tokens? Yes, and moreover: if the trading function (or a power of it) is polynomial, formulas can be obtained automatically using computational algebra systems, and in particular, using Groebner basis.

Groebner basis and LP fair price

If you studied linear algebra, you may recall that one way to solve a system of linear equations is to transform the system into a matrix and use the Gaussian elimination algorithm to put the system in a triangular form. One of the advantages of this method is that even if the solution of the system is not unique, this algorithm yields expressions that is simple to isolate one variable in function of others.

A similar algorithm exists for systems of polynomial equations: introduced in 1965 by Bruno Buchberger in his Ph.D. thesis, Buchberger's algorithm generalizes Gaussian elimination and computes a system of equations that is equivalent to the system of the original equations. The system obtained from Buchberger's algorithm, however, is much simpler, and it is the analogue of the triangular form resulting from Gaussian elimination.

Remark

Formally, the system obtained by Buchberger's algorithm is made by Groebner basis for (the ideal generated by the polynomials from) the original system. Other algorithms for computation of these basis exist, such as Faugere's F4 and F5 algorithm.

An excellent, self-contained book about this topic is "Ideals, varieties and algorithms" from David Cox, Donal O'Shea and John Little.

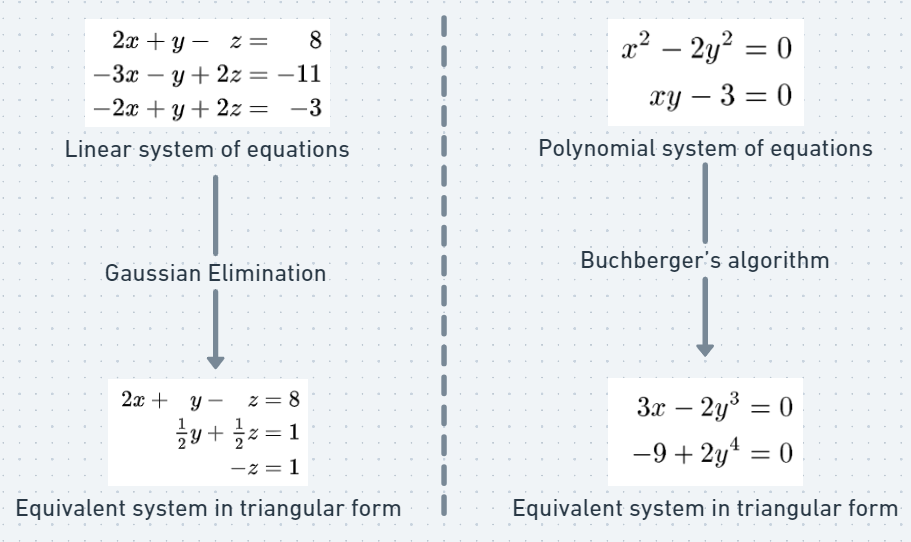
How can this algorithm be applied to get fair LP pricing formulas? We will illustrate using Mathematica and a weighted Balancer pool of 3 tokens as an example. For simplifying, we will admit that the fee of pool is 0.

Consider a pool whose trading function (in other words, its invariant) is given by:

$ \varphi(r_1,r_2,r_3)=r_1^{1/3} r_2^{1/3}r_3^{1/3} $

The spot price (or mid-price) $s_{ij}$ is the price at which you could theoretically trade an infinitesimal amount of token i for token j. For example, suppose that $\Delta r_1$ amounts of token 1 is sent to the pool in order to receive $\Delta r_3$ amounts of token 3. In order to satisfy the invariant function, we will have that

$ (r_1+\Delta r_1)^{1/3}r_2^{1/3}r_3^{1/3}=r_1^{1/3}r_2^{1/3}(r_3-\Delta r_3)^{1/3} $

This equation can be rewritten as

$ \begin{equation} \frac{\Delta r_3}{\Delta r_1} = \frac{r_3}{r_1 + \Delta r_1} \end{equation} $

As $\Delta r_1$ approximates 0, we have that the spot price $s_{13}$ is given by

$ s_{13} = \frac{\Delta r_3}{\Delta r_1} = \frac{r_3}{r_1} $

Remark

It is possible to calculate $s_{ij}$ systematically with computer algebra systems such as Mathematica. In Angeris, Guillermo et. al. is possible to find how to derive the following formula:

$ s_{ij} = \frac{[\nabla\varphi]_i}{[\nabla\varphi]_j} $

In our particular example,

$ \nabla\varphi(r_1,r_2,r_3)= \left(\frac{r_{2}^{1/3}r_{3}^{1/3}}{3r_{1}^{2/3}},\frac{r_{1}^{1/3}r_{3}^{1/3}}{3r_{2}^{2/3}},\frac{r_{1}^{1/3}r_{2}^{1/3}}{3r_{3}^{2/3}}\right) $

Supposing a no-arbitrage situation, the basis prices $p_{i}$ in USD and the spot price approximately satisfy $p_i = s_{ij} p_j$. In summary, we have the following system of polynomial equations for our example:

$ \begin{align} p_{1} - s_{13}p_{3} &= 0 \\ p_{2} - s_{23}p_{3} &= 0 \\ \varphi - K &= 0 \end{align} $

where K is the current invariant on the pool (which, usually, can be retrieved by communicating with its contract). We will use Mathematica, a Computer Algebra System (CAS), to describe these system of equations and Groebner basis to solve them:

The outputs of this command are Groebner basis: an expression that when it is equal to 0 is equivalent to our polynomial equations above, but easier to solve. Indeed, solving for each $r_i$ we obtain:

$ r_1 = K \frac{p_2^{1/3}p_3^{1/3}}{p_1^{2/3}}, \, r_2 = K \frac{p_1^{1/3}p_3^{1/3}}{p_2^{2/3}}, \, r_3 = K \frac{p_1^{1/3}p_2^{1/3}}{p_3^{2/3}} $

Remark

Note that Mathematica outputs two Groebner basis for each command: in our case both are equivalent since it is assumed that $r_i > 0$.

Finally, replacing the values of the LP price formula give us the fair price of the LP token:

$ LPP =\frac{\sum_{i=1}^{n} r_i p_i}{TS} =\frac{3Kp_1^{1/3}p_2^{1/3}p_3^{1/3}}{TS} $

To illustrate how this formula protects against flash loans (or whale movements) consider the weighted pool 33% DPI/33% WBTC/33% WETH, which the current state during the writing was approximately: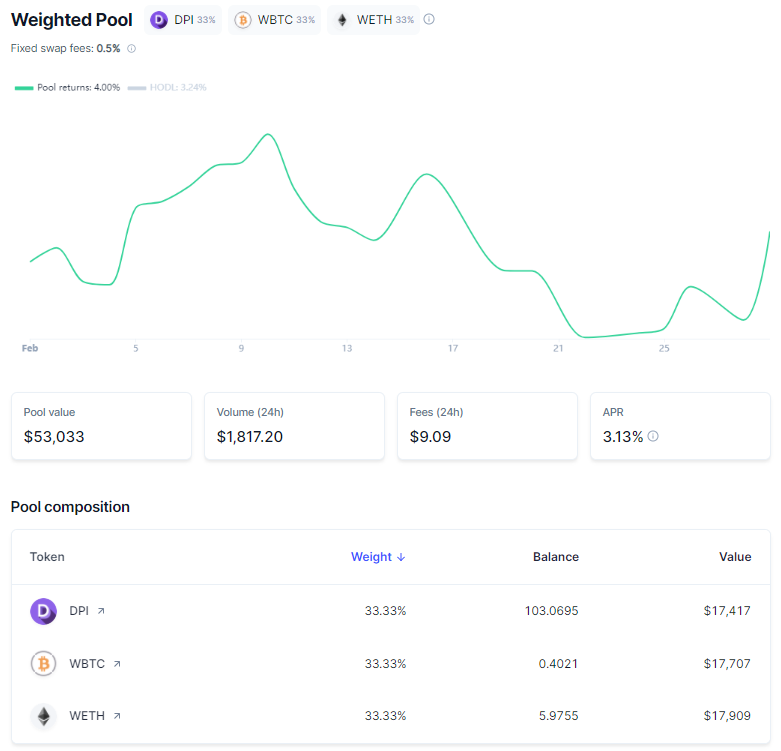

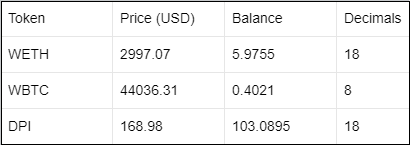
The LP token price can be estimated as:

$ \begin{align*} LPP & =\frac{\sum_{i=1}^{n} r_i p_i}{TS} \\ & =\frac{2997.07\times5.9755\times10^{18} +44036.31\times0.4021\times10^{8} +168.98\times103.0985\times10^{18}}{ 18.409563611131742132\times10^{18} } \\ &\approx 1920.06 \text{ USD} \end{align*} $

If a whale (or an user using a flash-loan) swaps almost all WETH from the pool by DPI, say $\Delta r_{3} = 0.9r_{3} = 5.37\text{ WETH}$, then equation (1) implies that $\Delta r_1=9r_1=927.81\text{ DPI}$. Immediately after the swap, the new LP token price ( $LPP_+$) will be:

• under the vulnerable formula

$ \begin{align*} LPP_+ &=\frac{10r_1p_1+r_2p_2+0.1r_3p_3}{TS} \\ &=\frac{10\times2997.07\times5.9755\times10^{18} +44036.31\times0.4021\times10^{8} +0.1\times168.98\times103.0985\times10^{18}}{ 18.409563611131742132\times10^{18} } \\ &\approx 9560.79\text{ USD}, \end{align*} $

almost 5x the original price.

• under the fair-price formula, however,

$ \begin{align*} LPP_+ &= \frac{3[(10r_1)^{1/3} r_2^{1/3}(0.1r_3)^{1/3}]p_1^{1/3}p_2^{1/3}p_3^{1/3}}{TS} \\ &=\frac{3[r_1^{1/3} r_2^{1/3}r_3^{1/3}]p_1^{1/3}p_2^{1/3}p_3^{1/3}}{TS} \\ &=\frac{3Kp_1^{1/3}p_2^{1/3}p_3^{1/3}}{TS} = LPP \end{align*} $

stays the same, as $K$ and the prices (immediately after) is unchanged by the swap.

Warning The text presented here does not prove that the fair pricing formula assures protection against hacks that could be caused by adding/removing a great quantity of liquidity in the pool - this will be further analyzed in another time and in another article.

Conclusion

In this article we saw how to use a Computer Algebra System (CAS) to automatically generate fair pricing formulas for protocols that needs to price a collateral asset. Further research could be done to automatically generate Solidity code based on the trading function of the pools. Indeed, as more complex DeFi protocols are launched, tools such as Groebner basis computation with CAS could turn out to be a useful tool for automating integrations, and consequently, easing interoperability between protocols.

References

1. Alpha Finance's blog: Fair Uniswap's LP Token Pricing

2. Christoph Michel's blog: Pricing LP tokens | Warp Finance hack

3. Angeris, Guillermo, et al. "Constant function market makers: Multi-asset trades via convex optimization." arXiv preprint 2107.12484 (2021).

4. Cox, David, John Little, and Donal O'Shea. Ideals, varieties, and algorithms: an introduction to computational algebraic geometry and commutative algebra. Springer Science & Business Media, 2013.

Acknowledgements

I would like to give a special thanks to Mikko Ohtama and André Pereira for kindly reviewing this post and for their helpful suggestions.