As an alternative to VertexDelete, the new SubgraphExpand allows a little more flexibility and positivity to users wishing to explore structures internal to a Graph.

SubgraphExpand = ResourceFunction["SubgraphExpand"] ;

As a test case, let's look at a semi-random graph generated by transforming an algebraic curve to a mesh of polygons:

AnharmonicOscillator = DiscretizeRegion[ImplicitRegion[
0 == GroebnerBasis[
       {1/2 == -u^2 - v^2 - u^2 v^2 + x^2 + v^2 x^2 + 4 u v x y + 
          y^2 + u^2 y^2 - x^2 y^2,
        0 ==  2 u x + 2 u v^2 x + 2 v y + 2 u^2 v y - 2 v x^2 y - 2 u x y^2,
        z^2 == x^2 + y^2 + u^2 + v^2}, {x, y, z}, {u, v}][[1]],
    {x, y, z}], {{-3/4, 3/4}, {-3/4, 3/4}, {-2, 2}}];
graph0 = Graph3D[MeshConnectivityGraph[AnharmonicOscillator, 2]];
AnharmonicOscillator -> GraphPlot[graph0] 

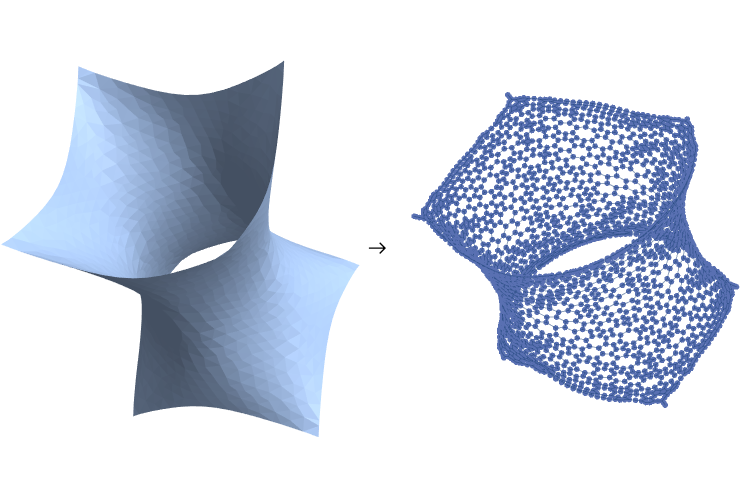
We can immediately choose a random point and expand:

SeedRandom["EquatorTest"];
v0 = RandomChoice[VertexList[graph0]];
expansion = Graph[SubgraphExpand[graph0, {v0}, #]] & /@ (5 Range[8]);
Grid[Partition[expansion, 4], Frame -> All, FrameStyle -> LightGray, 
 Spacings -> {1, 1}]

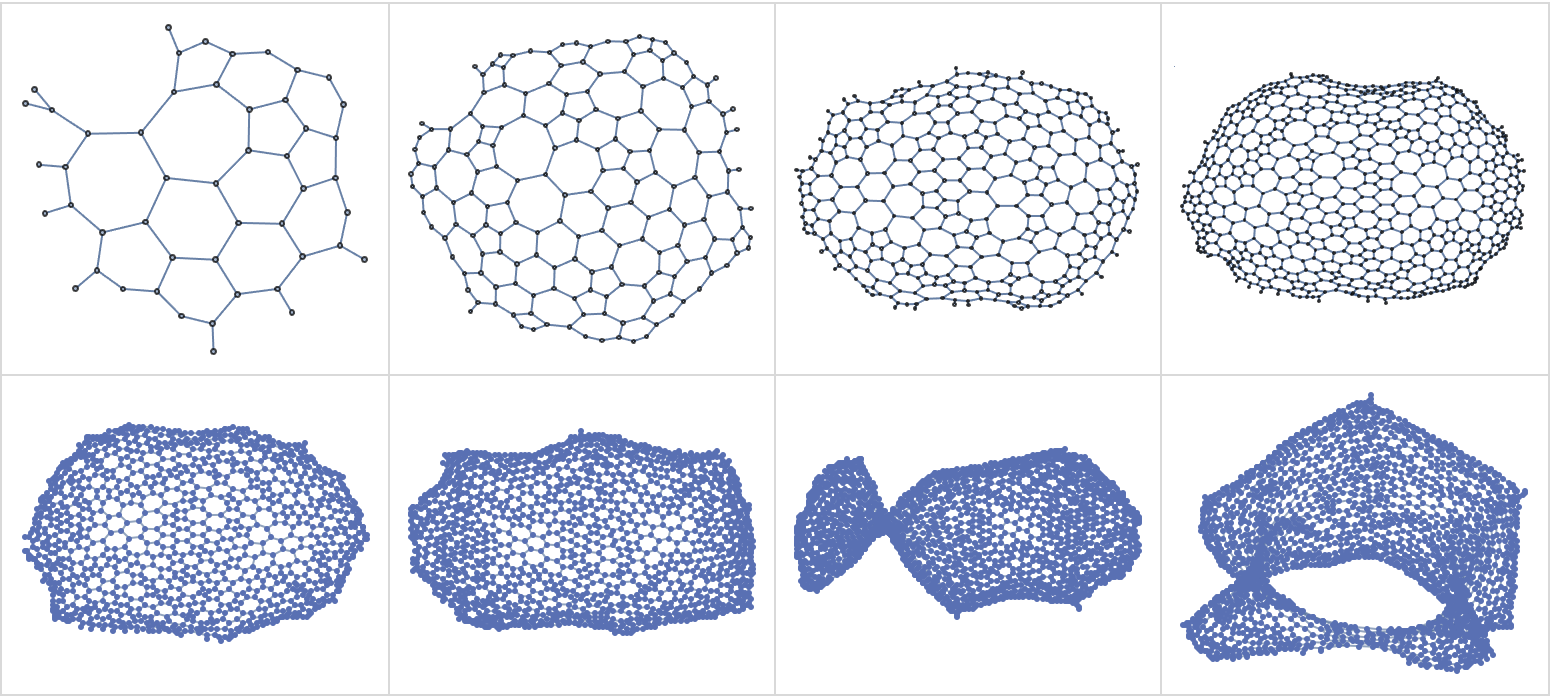
But this is not exactly what we want for potential physics applications. Notice that the two dimensional surface has a circumference whose graph diameter is about 40. Our goal is to find a cycle around the circumference, and use it to expand a thin strip. This can be done by finding near vertices on one subgraph, which appear far on another.

v40 = Select[VertexList[graph0], GraphDistance[graph0, v0, #] == 40 &];
v39 = Select[VertexList[graph0], GraphDistance[graph0, v0, #] == 39 &];

data = With[{sg = SubgraphExpand[graph0, {v0}, 39]},
   Outer[GraphDistance[sg, #1, #2] &, v39, v39, 1]];

pos2 = Position[With[{sg = SubgraphExpand[graph0, {v0}, 40]},
    Outer[GraphDistance[sg, #1, #2] &, v39, v39, 1]], 2];

nearDiameterPoints = 
  v39[[pos2[[#]]]] & /@ 
   Flatten[Position[data[[Sequence @@ #]] & /@ pos2,
     Max[data[[Sequence @@ #]] & /@ pos2]]];

HighlightGraph[g40, nearDiameterPoints[[5]]];

diameterGraph = Graph[UndirectedEdge @@@ Partition[
     Join[
      FindShortestPath[g39, nearDiameterPoints[[5, 1]], 
       nearDiameterPoints[[5, 2]]], 
      FindShortestPath[g40, nearDiameterPoints[[5, 2]], 
        nearDiameterPoints[[5, 1]]][[2 ;; 3]]], 2, 1]];

Graph3D[HighlightGraph[graph0,
  SubgraphExpand[graph0, diameterGraph, 2]]]

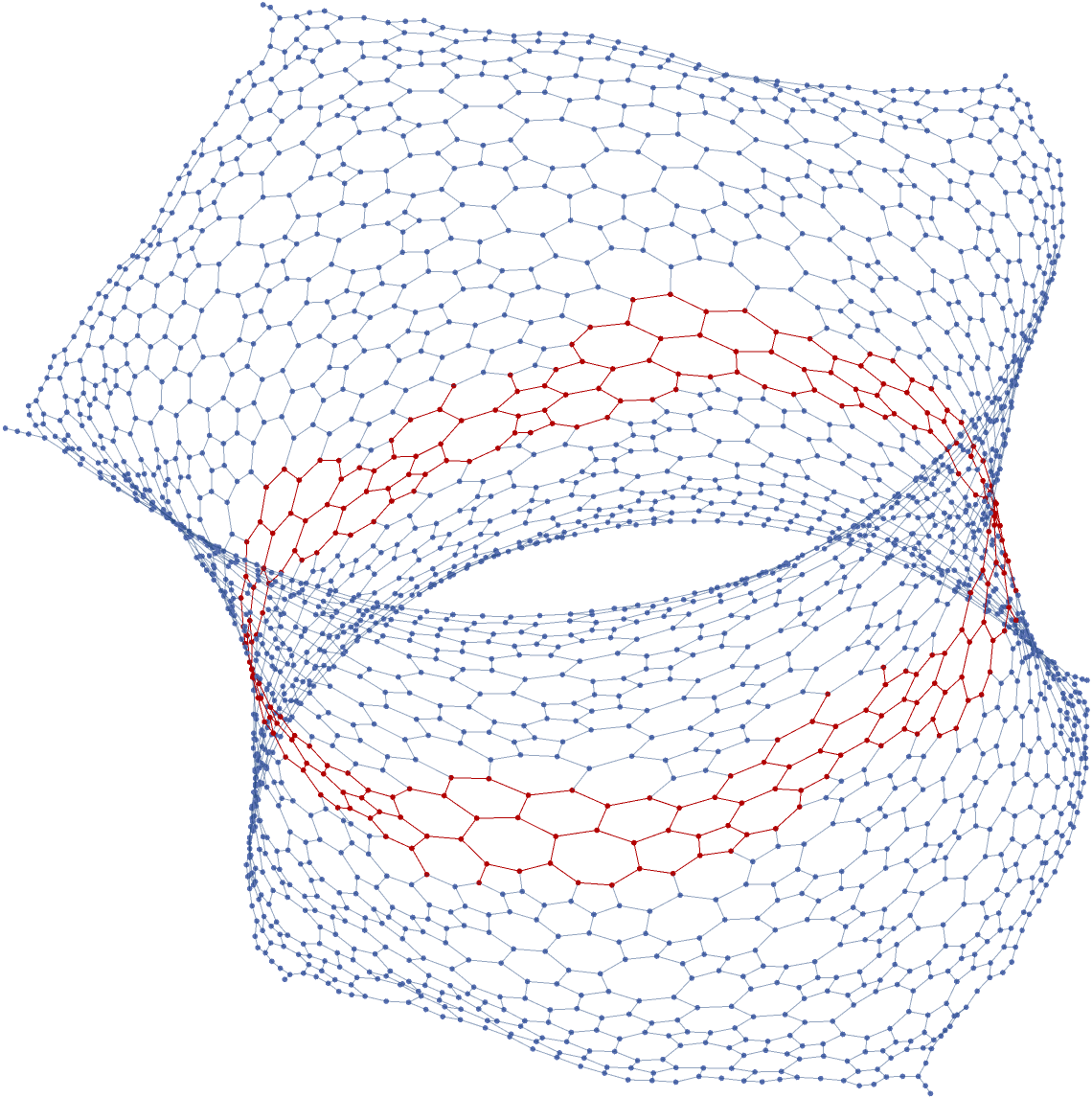
Perhaps this is a nice domain for some sort of quantum oscillator, but we don't know without more details.

What's more clear from this exercise is that it might be worthwhile to develop a new FindCycle function, which has an optional parameter "NonContracting". Setting "NonContracting" to True, would then cause the search to look only for those cycles which do not contract to facet boundaries.