Laplacian Equation

I want to conduct seepage analysis in Mathematica. See the model in the screenshot and the attached notebook. The problem is to find the numerical solution of the Laplacian equation.

solution = NDSolveValue[{\!\(
\*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == 
    NeumannValue[0, y == 0] + NeumannValue[0, x == 0] + 
     NeumannValue[0, x == width] + 
     NeumannValue[0, 
      y == height && (width/3 < x < (2 width)/3)], {dcond1, dcond2}}, 
  u, {x, y} \[Element] \[CapitalOmega]]

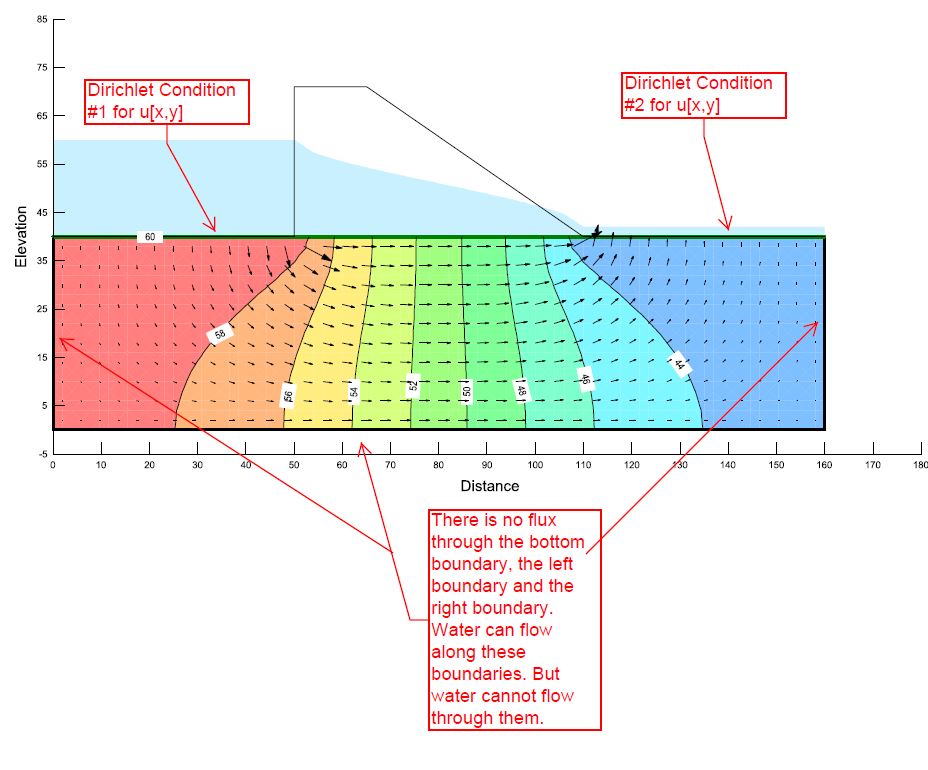
Neumann Boundary Condition

Note that the region is a rectangle. As shown in the screenshot, there is no flux through the left boundary, the right boundary and the bottom boundary. However, water can flow along these boundary. See the first screenshot.

Incorrect Results

The second screenshot shows incorrect results. I checked the gradient of u[x,y].

v = Grad[-solution[x, y], {x, y}]

I see the vector field is incorrect. The NeumannValue function is not working in the notebook. See the vector plot which presents the result of v. 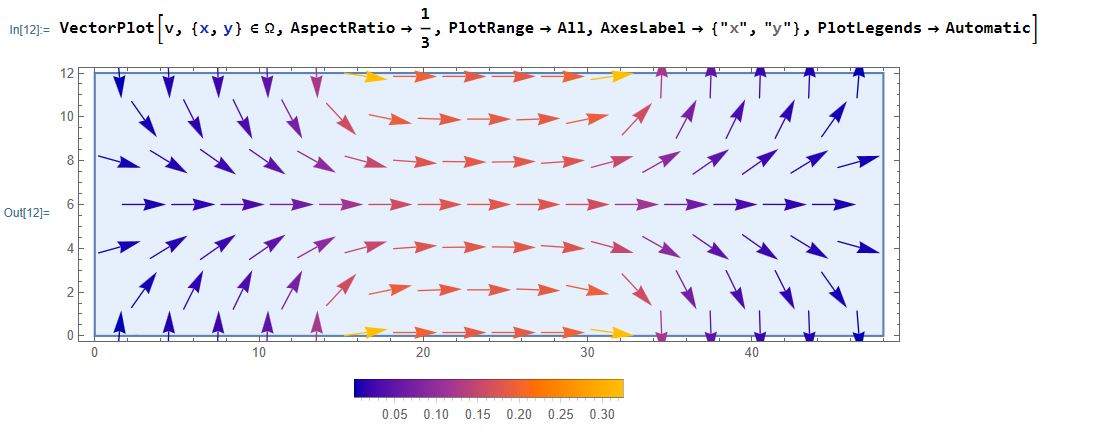How should I add Neumann Boundary Conditions to produce similar results in the first screenshot.