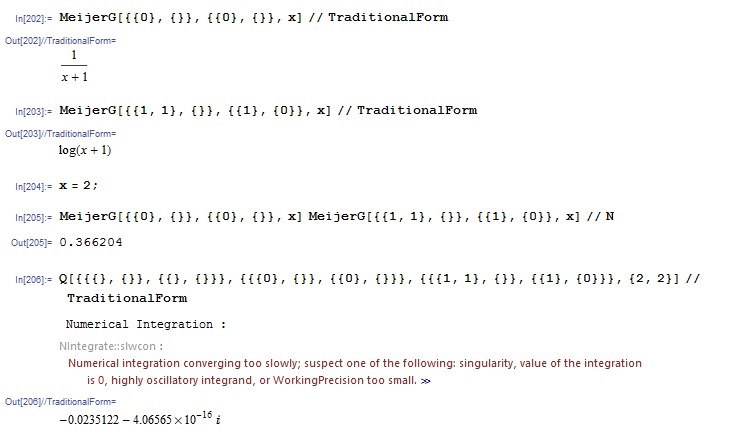
I am trying to validate https://functions.wolfram.com/07.34.16.0003.01. Mathematica result: -0.0235122-4.06565*10^-16 I and Manual result: 0.366... Please help me to match both values.

Q[{{{}, {}}, {{}, {}}}, {{{0}, {}}, {{0}, {}}}, {{{1, 
     1}, {}}, {{1}, {0}}}, {2, 2}] // N

(*Extended Generalized Bivariate Meijer G-Function (EGBMGF)*)
 Clear All;
(*Exception*)
Q::InconsistentCoeffs = " Inconsistent coefficients ";
Q[{cst_, dst_}, {cs_, ds_}, {ct_, dt_}, {zs_, zt_}] := Module[{},
    (*Only's' is used as argument in the Gamma product terms along \
with other parameters*) 
    Eas = 
    Function[v, 
     Product[Gamma[1 - cs[[1, n]] + v], {n, 1, Length[cs[[1]]]}]];
    Fas = 
    Function[v, 
     Product[Gamma[cs[[2, n]] - v], {n, 1, Length[cs[[2]]]}]];
    Ebs = 
    Function[v, 
     Product[Gamma[ds[[1, n]] - v], {n, 1, Length[ds[[1]]]}]];
    Fbs = 
    Function[v, 
     Product[Gamma[1 - ds[[2, n]] + v], {n, 1, Length[ds[[2]]]}]];
    Ps = Function[v, Eas[v] Ebs[v]/(Fas[v] Fbs[v])];
    (*Only't' is used as argument in the Gamma product terms along \
with other parameters*) 
    Eat = 
    Function[v, 
     Product[Gamma[1 - ct[[1, n]] + v], {n, 1, Length[ct[[1]]]}]];
    Fat = 
    Function[v, 
     Product[Gamma[ct[[2, n]] - v], {n, 1, Length[ct[[2]]]}]];
    Ebt = 
    Function[v, 
     Product[Gamma[dt[[1, n]] - v], {n, 1, Length[dt[[1]]]}]];
    Fbt = 
    Function[v, 
     Product[Gamma[1 - dt[[2, n]] + v], {n, 1, Length[dt[[2]]]}]];
    Pt = Function[v, Eat[v] Ebt[v]/(Fat[v] Fbt[v])];
    (*'s+t' is used as argument in the Gamma product terms along with \
other parameters*) 
   East = 
    Function[v, 
     Product[Gamma[cst[[1, n]] + v], {n, 1, Length[cst[[1]]]}]];
    Fast = 
    Function[v, 
     Product[Gamma[1 - cst[[2, n]] - v], {n, 1, Length[cst[[2]]]}]];
    Fbst = 
    Function[v, 
     Product[Gamma[dst[[2, n]] + v], {n, 1, Length[dst[[2]]]}]];
    Pst = Function[v, East[v]/(Fast[v] Fbst[v])];
    MT = Function[{v, w}, Ps[v] + Pt[w]/Pst[v + w]];
    (*Countour limiters (The Gamma arguments in the numerator \
determine the value of the limiters which must be half of the least \
valued Gamma arguments)*) 
   As = 1/4;
    At = 1/4;
    Zs = zs;
    Zt = zt;
    W = 50;
    (*The final value is calculated*) 
   Print[" Numerical Integration :"];
    value = 
    1/((2 \[Pi] I)^2) NIntegrate[
      MT[s, t] Zs^s Zt^t, {s, As - I W, As + I W}, {t, At - I W, 
       At + I W}];
    (*The value is returned*) 
   Return[value];
   ];
(*End of EGBMGF*)

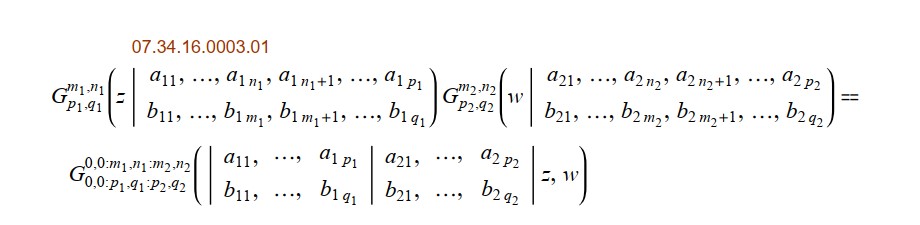
Attachments:

Screenshot_4.jpg

Screenshot_5.jpg

Screenshot_6.jpg