A question about the new Stephen Wolfram blog post, Via reddit, andrewl_ :
Are these any different than game trees?
A: If you really want to know, do the calculations!
Thanks to Click-to-copy and WFR, it should be easier than ever to try and keep up. Admittedly, there is a slight delay in getting source code + documentation published. In the meantime we can at least use the fully-functional Click to Copy. In all of the following functions wrapped by C2C[fun] can be grabbed from the blog post or the attached notebook (thanks Nik!):
TreeQ[C2C[TTTData]["GameGraph"]]
Out[]=False
It would be nice if the following actually worked, but it doesn't:
TimeConstrained[
gameTree = C2C[MultiwayDeletionsGraph][C2C[TTTData]["GameGraph"]],
60]
Not my fault! According to wikipedia, this Tree Graph should have 255,168 leafs, which could probably mean 500K+ vertices in total--And we don't really want to sit around waiting for that to compute.
Instead we can just count unique the paths through the DAG using DirectedAcyclicEvaluate::
PathCountTTT = Association[
ResourceFunction["DirectedAcyclicEvaluate"][
C2C[TTTData]["GameGraph"], {_List :> 1}
]["VertexWeights"]];
And use this meta-data to get the big numbers:
Total[PathCountTTT[#] & /@ Join[
Flatten[Values[C2C[TTTData]["FirstWinStates"]], 1],
C2C[TTTData]["DrawStates"][9]]]
Out[] = 255168
Total[Values[PathCountTTT]]
Out[]= 549946
But as a further example, let's try MultiwayDeletionsGraph on the 2x2 X's and O's game. In fact, we don't even need NestWhileGraph because the state space is small and easy to enumerate directly:
gtt1 = Graph[ResourceFunction["ToDirectedAcyclicGraph"][
NearestNeighborGraph[Select[
Tuples[{-1, 0, 1}, 4], 0 <= Total[#] < 2 &] ], {0, 0, 0, 0}],
VertexCoordinates -> Automatic,
GraphLayout -> "LayeredDigraphEmbedding"]
gtt2 = Graph[C2C[MultiwayDeletionsGraph][gtt1, {{0, 0, 0, 0}}],
GraphLayout -> "LayeredDigraphEmbedding",
AspectRatio -> 1/2]
Out[]=
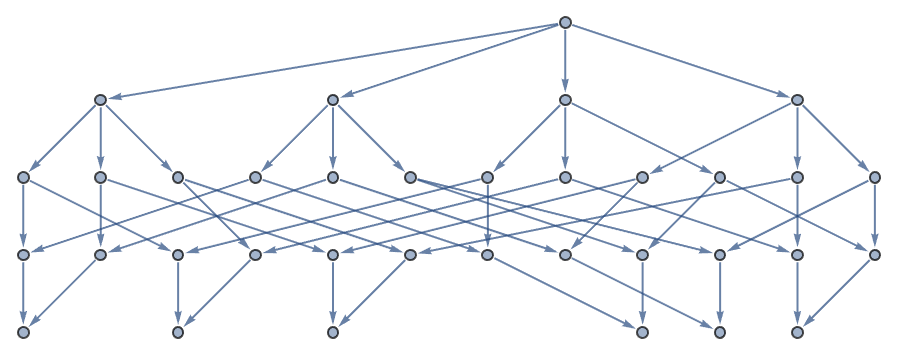
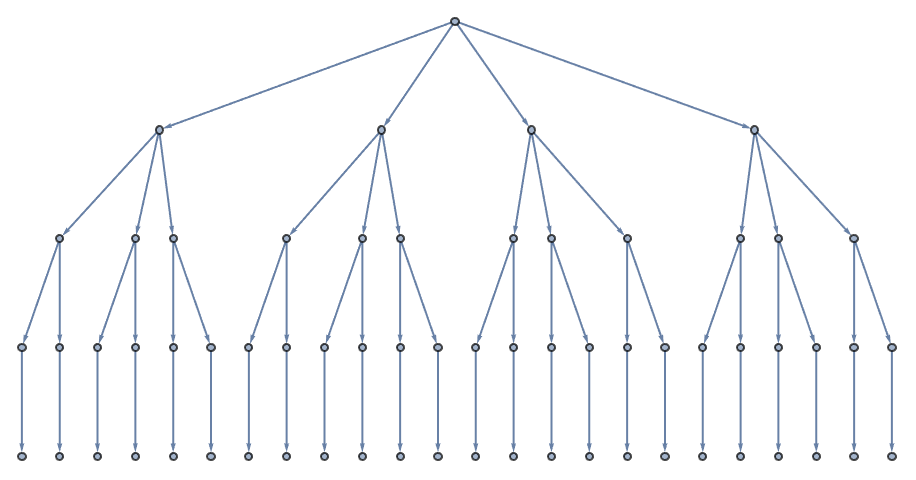
And you can easily verify in this particular case that path count on the DAG equals leaf count on the tree. But what is actually happening here? And what is happening in general?
The new state-space exploring function MultiwayDeletionsGraph (soon to be a WFR) typically does not produce TreeGraph outputs. Blog sections "Walks and Their Multiway Graphs" and "The Icosian Game & Some Relatives" show examples from the more general case where exploration paths can be confluent by first branching apart and later merging together. However, the inputs in subsequent sections are state spaces without time ordering. What happens in general is that two paths visit the same graph components but in different order, but that certainly can not happen if vertices are uniquely associated with a time.
In the case of a directed acyclic input to MultiwayDeletionsGraph, I think it is not too difficult to prove that the output must be a tree, and if the input DAG is a game DAG, then the output tree is a game Tree. In every such case I would expect that pathcount via DirectedAcyclicEvaluate should give the same answer as leaf count on the game tree.
However, what we really want to know about is FAIRNESS, another metric computable by DirectedAcyclicEvaluate. Fairness is related to partial probabilities by time reversal symmetry. In fact, there is a nice theorem with obvious analogs about time-ordered, quantum mechanical propagators, which regrettably did not make it past the outline stage of the writing process. :( As is often said, more work remains to be done...