Thank you Gianluca for your time.
Actually, I reformed my code myself like this:
\[Kappa] = 4; \[Gamma]0 = 1/10; \[Sigma]0 = 1/5; \[Theta] = 6/5;
H = 1/2 + 1/6; \[Rho] = -(3/4); K = 115;
Subscript[S, 0] = 100; r = 953/10000; T = 1/2;
F0[t_] := Subscript[S, 0]*E^(r*t)
Ktilde[t_] := 1 - K/F0[t]
E1[t_] := E^(\[Kappa]*t)
Ebar[t_] := E^(-\[Kappa]*t)
L0[t_] := \[Sigma]0*Ebar[t] + ((1 - Ebar[t])*\[Theta])/\[Kappa]
f0[t_] := L0[t]
Subscript[\[Lambda], 1][t_, s_] := (t - s)^(H - 1/2)/Gamma[H + 1/2]
Subscript[\[Lambda], 2][t_,
s_] = \[Gamma]0*(Subscript[\[Lambda], 1][t,
s] - \[Kappa]^(1/2 - H) *E1[s]*Ebar[t]*
Integrate [x^(H - 1/2) E^x, {x, 0, (t - s) \[Kappa]},
Assumptions -> (t - s) \[Kappa] > 0]) // FullSimplify
Vbar[s_] =
f0[s] + \[Rho]*
Integrate[f0[u] *Subscript[\[Lambda], 2][s, u], {u, 0, s},
Assumptions -> s > 0] // FullSimplify
\[CapitalSigma][T] = NIntegrate[(Vbar[s])^2, {s, 0, T}]
when I reformed the code, I could compute Vbar[s_] and Subscript[[Lambda], 2][t,
s] symbolically. Even I could compute [CapitalSigma][T] numerically. you can see our result in the below picture:

It seems good. But now there is just another problem and it's when we want to compute q_1
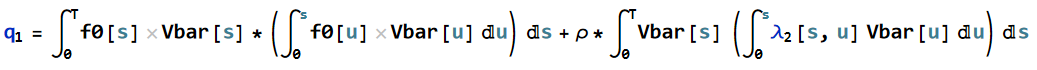
. As you can see in q_1 when we want to compute each side of the plus sign numerically, there is an inner integral and it can't be computed. So outer integral can't be computed numerically as well.
I think the inner integral should be computed symbolically but it doesn't answer.
How can we compute q_1 numerically? any suggestions?