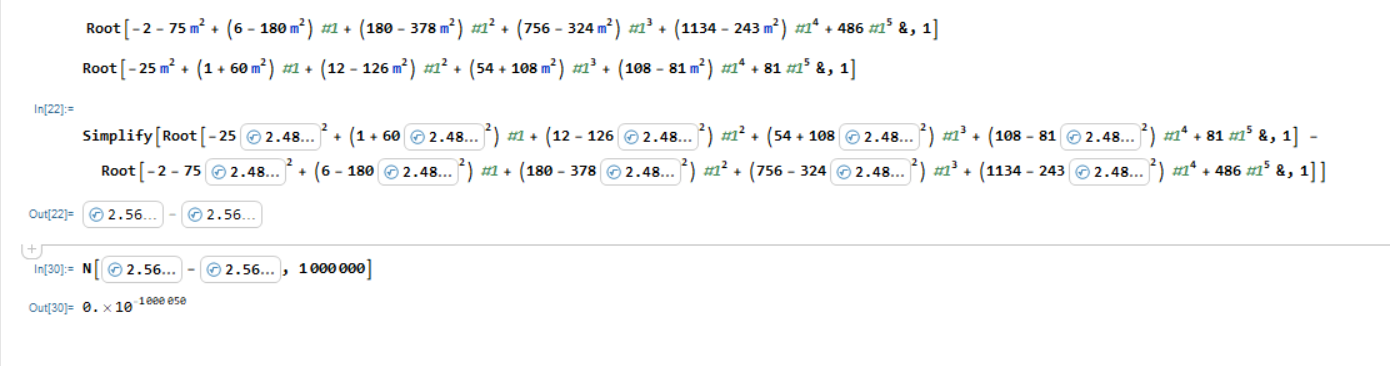
I have the two following Root functions that I wish to evaluate at the same m value as I believe them to be the same for several reasons, one of which is that I've graphed the functions and it looks like it as well. I've provided a picture of what it looks like in my Notebook as it is a lot easier on the eyes for digesting the problem. The question is, "Is this zero like I think it is, and if so, why can't I seem to get zero as an exact solution?"

 Root[-2 - 
   75 m^2 + (6 - 180 m^2) #1 + (180 - 378 m^2) #1^2 + (756 - 324 m^2) #1^3 + (1134 - 243 m^2) #1^4 + 486 #1^5 &, 1]

Root[-25 m^2 + (1 + 60 m^2) #1 + (12 - 126 m^2) #1^2 + (54 + 108 m^2) #1^3 + (108 - 81 m^2) #1^4 + 81 #1^5 &, 1]

Usually when I think something is the same at a value, I check by either a ReplaceAll (which doesn't work well in this case) or plugging in by hand and using Simplify. The m value that I wish to use is:

Root[32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 0]

However, when I plug this into one root function minus another using simplify like so:

In[22]:= 
Simplify[Root[-25 Root[
      32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 
       0]^2 + (1 + 
        60 Root[32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #\
^6 - 220725 #^8 + 151875 #^10& , 4, 0]^2) #1 + (12 - 
        126 Root[
         32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 0]^2) #1^2 + (54 + 
        108 Root[
         32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 0]^2) #1^3 + (108 - 
        81 Root[32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #\
^6 - 220725 #^8 + 151875 #^10& , 4, 0]^2) #1^4 + 81 #1^5 &, 1] - 
  Root[-2 - 
     75 Root[32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #\
^6 - 220725 #^8 + 151875 #^10& , 4, 
       0]^2 + (6 - 
        180 Root[
         32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 0]^2) #1 + (180 - 
        378 Root[
         32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 0]^2) #1^2 + (756 - 
        324 Root[
         32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 0]^2) #1^3 + (1134 - 
        243 Root[
         32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , 4, 0]^2) #1^4 + 486 #1^5 &, 1]]

Out[22]= Root[{
  32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , \
(-25) #^2 + #2 + 60 #^2 #2 + 12 #2^2 - 126 #^2 #2^2 + 54 #2^3 + 108 #\
^2 #2^3 + 108 #2^4 - 81 #^2 #2^4 + 81 #2^5& }, {4, 1}] - Root[{
  32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , \
-2 - 75 #^2 + 6 #2 - 180 #^2 #2 + 180 #2^2 - 378 #^2 #2^2 + 756 #\
2^3 - 324 #^2 #2^3 + 1134 #2^4 - 243 #^2 #2^4 + 486 #2^5& }, {4, 1}]

which appears to be zero as seen here:

In[30]:= N[
 Root[{32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , \
(-25) #^2 + #2 + 60 #^2 #2 + 12 #2^2 - 126 #^2 #2^2 + 54 #2^3 + 108 #\
^2 #2^3 + 108 #2^4 - 81 #^2 #2^4 + 81 #2^5& }, {4, 1}] - 
  Root[{32768 - 2020986 #^2 - 10826991 #^4 - 2570157 #^6 - 220725 #\
^8 + 151875 #^10& , \
-2 - 75 #^2 + 6 #2 - 180 #^2 #2 + 180 #2^2 - 378 #^2 #2^2 + 756 #\
2^3 - 324 #^2 #2^3 + 1134 #2^4 - 243 #^2 #2^4 + 486 #2^5& }, {4, 
   1}], 1000000]

Out[30]= 0.*10^-1000050