The problem I want to solve here is as follows: Based on the representation matrices of O(3) group elements, find/identify/determine the possible bases on which they depend.

More specifically, in the example I posted above, {{0, -1, 0}, {0, 0, -1}, {-1, 0, 0}} is the matrix representation of a O(3) group element. I want to determine the possible basis with the help of eigen system analysis. My idea comes from the example provided in the official document of Eigensystem:

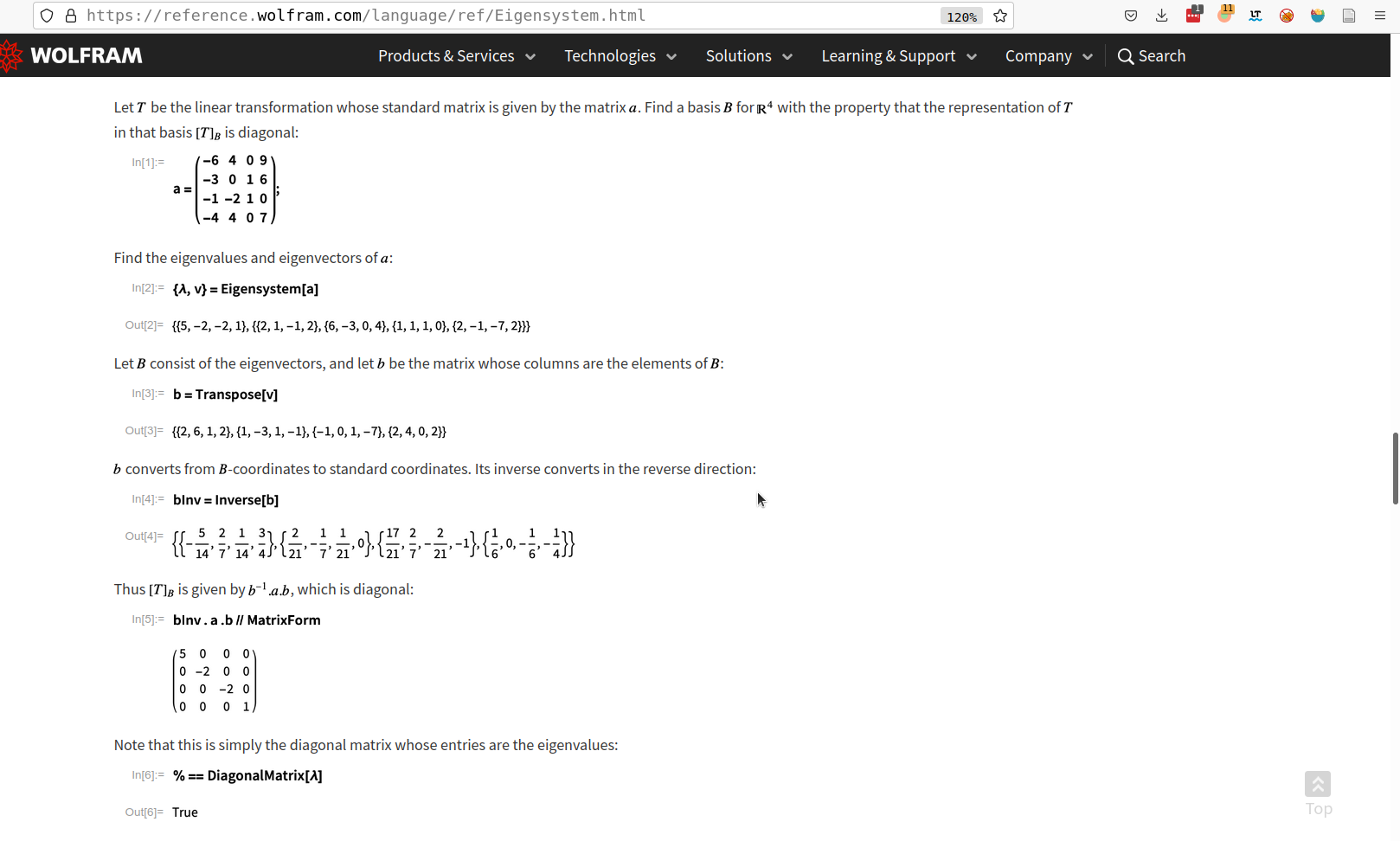
However, in my question, these group elements are point groups of a space group, so their bases cannot be selected arbitrarily. This also means that the volume of the parallelepiped formed by the corresponding basis vectors must meet specific requirements. Therefore, it means that the length of the corresponding eigenvector must be specific rather than arbitrarily selected. Therefore, this leads to the question I am asking here.

For the above reasons, I do not know whether the eigen system analysis method can find the specific lattice basis of a space group. If not, whether there is a better way, or I can further adjust the default behavior of the Eigensystem command to meet my needs.

Any hints will be appreciated.

Regards, Zhao