I try to reproduce the example 5 given here:
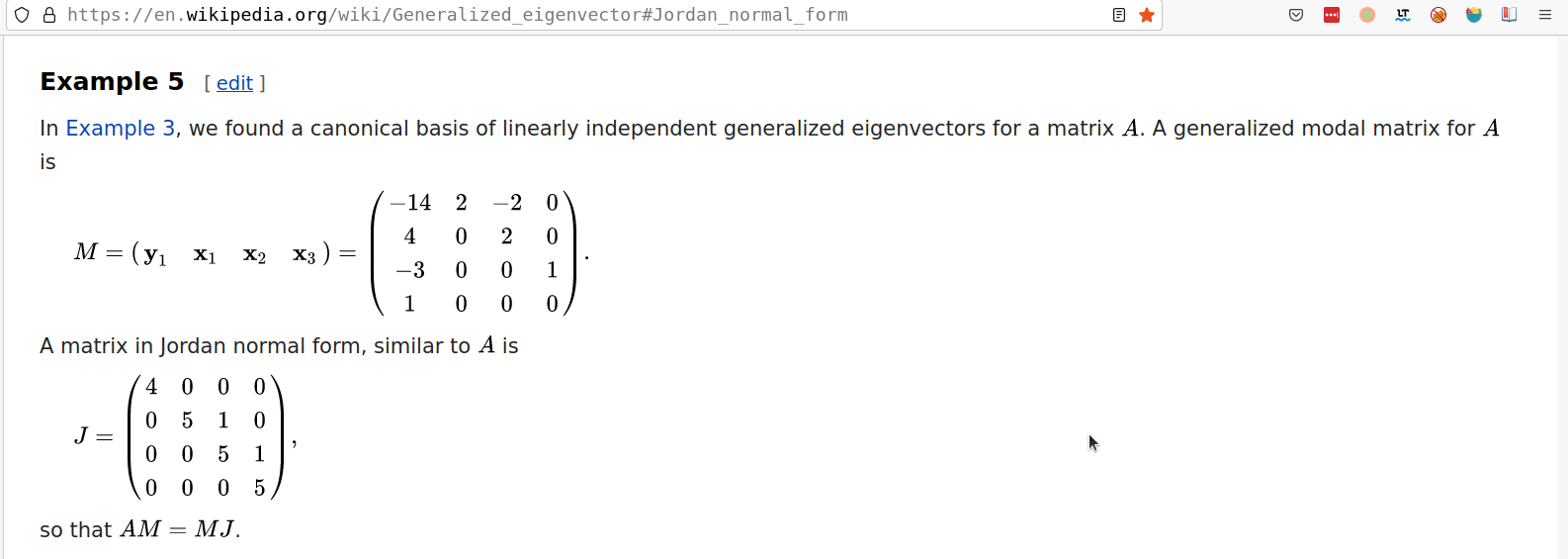
In[173]:= (*Example 5*)
mA={{-14,2,-2,0},{4,0,2,0},{-3,0,0,1},{1,0,0,0}}
mA//JordanDecomposition//RootReduce
Out[173]= {{-14, 2, -2, 0}, {4, 0, 2, 0}, {-3, 0, 0, 1}, {1, 0, 0, 0}}
Out[174]= {{{Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 1, 0],
Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 2, 0],
Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 3, 0],
Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 4, 0]}, {Root[
462 - 274 # + 48 #^2 - 11 #^3 + 2 #^4& , 2, 0], Root[
462 - 274 # + 48 #^2 - 11 #^3 + 2 #^4& , 1, 0], Root[
462 - 274 # + 48 #^2 - 11 #^3 + 2 #^4& , 3, 0], Root[
462 - 274 # + 48 #^2 - 11 #^3 + 2 #^4& , 4, 0]}, {Root[
29 + 124 # + 104 #^2 + 34 #^3 + 4 #^4& , 1, 0], Root[
29 + 124 # + 104 #^2 + 34 #^3 + 4 #^4& , 2, 0], Root[
29 + 124 # + 104 #^2 + 34 #^3 + 4 #^4& , 4, 0], Root[
29 + 124 # + 104 #^2 + 34 #^3 + 4 #^4& , 3, 0]}, {1, 1, 1,
1}}, {{Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 1, 0], 0, 0,
0}, {0, Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 2, 0], 0, 0}, {0,
0, Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 3, 0], 0}, {0, 0, 0,
Root[-4 + 14 # - 14 #^2 + 14 #^3 + #^4& , 4, 0]}}}
As shown above, I got a very complicated result and couldn't get the simple form given in the Wiki. Any tips for solving this problem?
Regards,
Zhao