Here is an attempt with a[i] a vector instead of a scalar:

f[a_, n_, x_] := Sum[a[i] . { Cos[i x], Sin[i x]}, {i, 1, n}]
innerManipulate[n_Integer] := 
  Manipulate @@ {Graphics[
     Line@Table[{x, f[a, n, x]}, {x, -2 \[Pi], 2 \[Pi], .1}], 
     Axes -> True], 
    Sequence @@ 
     Table[{{a[i], {0, 0}}, {-1, -1}, {1, 1}}, {i, 1, n}]};
Manipulate[innerManipulate[n], {n, 1, 5, 1, SetterBar}]

Hello Eric, hello Gianluca,

Thanks a lot for your help - I realize I'm not really comfortable with Mathematica advanced syntax! I was able to run your codes and to adapt yours Gianluca to my actual problem: manipulating Fourier series.

f[a_, b_, n_, x_] := Sum[a[i] Cos[i x] + b[i] Sin[i x], {i, 1, n}]
innerManipulate[n_Integer] := 
  With[{cntrls = 
     Flatten[Table[{{{a[i], 0}, -1, 1}, {{b[i], 0}, -1, 1}}, {i, 1, 
        n}], 1]}, 
   Manipulate @@ {Graphics[
      Line@Table[{x, f[a, b, n, x]}, {x, -2 \[Pi], 
         2 \[Pi], .1}], Axes -> True], Sequence @@ cntrls}];
Manipulate[innerManipulate[n], {n, 1, 5, 1}]

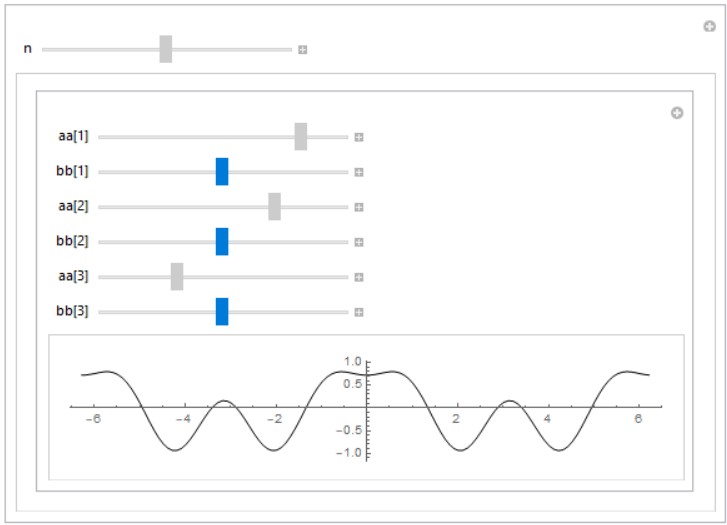Eric I don't know why I wasn't able to adapt your code, it looks like something gets wrong sometimes with initialization...

I'll now try to use Slider2D for Fourier coefficients so that it looks nicer - but I feel like it's going to be more than just a quick cosmetic change :D

Thank you again!

Your code doesn't work because your local variables aren't lining up as you expect. Also, I don't think Manipulate likes it when the control variables depend on other control variables. When you have such dependencies, you can workaround this by making your own controls explicitly (look at all of the forms of controls at http://reference.wolfram.com/language/guide/ControlObjects.html).

For your case, you might be able to avoid the nested Manipulate by doing something like this:

Manipulate[
 Grid[
  {{Grid[{HoldForm[a[#]], Slider[Dynamic[a[#]], {0, 1}]} & /@ 
      Range[n]]},
   {f[a, n, x]}}],
 {n, 1, 3, 1}]

This isn't polished. There are some weird effects trying to interact with the sliders, and there's no initialization for each a[n], but maybe this will give you a path to follow.