Sandor,
I am assuming you just want a numerical solution. Here is one simple way:
n=5;
lineLoop = ParametricPlot3D[{(2 + Cos[n u]) Cos[u], (2 + Cos[n u]) Sin[u], Sin[n u]}, {u, 0, 2 Pi}];
length = RegionMeasure@DiscretizeGraphics[lineLoop]
(* Out: 34.0784 *)
Regards -- Henrik
ADDENDUM:
Well, I guess my approach above was a quite lazy one - things can be done better:
loopFunc[n_][t_] := {(2 + Cos[n t]) Cos[t], (2 + Cos[n t]) Sin[t], Sin[n t]};
ClearAll[v, n, t];
v[n_][t_] = D[loopFunc[n][t], t];
loopLength[n_?NumericQ] := NIntegrate[Norm[v[n][t]], {t, 0, 2 Pi}]
With this you get e.g. for winding number 5:
loopLength[5]
(* Out: 34.0869 *)
which is probably more exact than the other value above.
The loop length depending of the winding number is surprisingly not a monotone function:
(* length in terms of the respective full circle: *)
Plot[loopLength[n]/(6 Pi), {n, 0, 10}, PlotRange -> {0, Automatic}, GridLines -> {Range[10], None}]
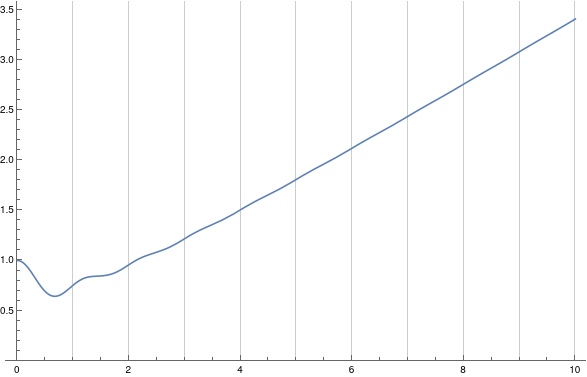
FindMinimum[loopLength[n], n]
(* Out: {12.12186, {n -> 0.6715288}} *)
But one can convince oneself that this seems to be correct:
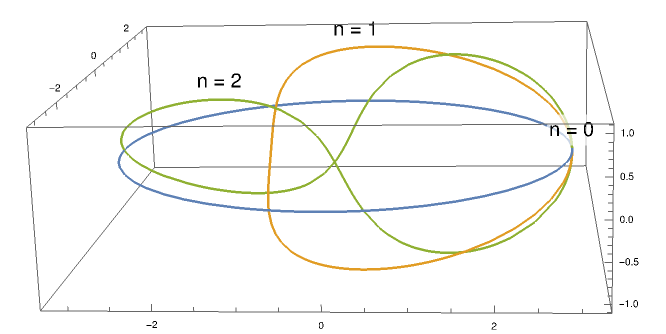
ParametricPlot3D[{loopFunc[0][t], loopFunc[1][t], loopFunc[2][t]}, {t,0, 2 Pi},
PlotLabels -> Placed[Style[#, 20] & /@ {"n = 0", "n = 1", "n = 2"}, Above]]