In a previous thread we found that it is not too difficult, but also not very easy to Classify parts of 2D SNES maps in terms of their heights. What's much easier is to simply make our own voxelized height map, and use such a geometry as the scene of game involving voxel chess pieces. The purpose of this memo is to build on Keying's initial game design study by showing how to automate camera and character control by key pressing.
First we need to import pieces:
ToCubes[verts_, cols_] := With[
{colRep = Rule[#[[1]], RGBColor[#[[2 ;; 4]]/255]] & /@ cols},
{#[[4]] /. colRep,
Cuboid[(#[[1 ;; 3]] + {4, 4, 0})/8, (#[[1 ;; 3]] + {5, 5, 1})/
8]} & /@ verts]
ImportVox[file_] := With[
{lines = StringSplit[Import[file], "\n"]}, Function[{markers},
ToCubes[Map[ToExpression, DeleteCases[
StringSplit[lines[[markers[[2]] + 1 ;; markers[[3]] - 1]],
" "], "", Infinity], {2}],
Map[ToExpression,
DeleteCases[StringSplit[lines[[markers[[4]] + 1 ;; -1]],
" "], "", Infinity], {2}]]][
Flatten[Position[lines, "---------------------"]]]]
AbsoluteTiming[
primitives = MapApply[RegionUnion, Map[Last, SortBy[GatherBy[ImportVox[
"https://raw.githubusercontent.com/bradklee/OpenAssets/main/WorldChess/TXT/Y" <> # <> "Vox.txt"
], First], Length], {2}]] & /@ {"Pawn", "Rook", "Knight", "Bishop", "Queen", "King"};]
Graphics3D/@primitives

(perhaps we should just make a WFR for these?)
Next we generate the setting:
HeightRules[mazeData_] := Module[{
g1 = NearestNeighborGraph[Position[mazeData, 5]],
wallComponents = WeaklyConnectedComponents[
NearestNeighborGraph[Position[mazeData, 0],
{4, 1}]], heightRulesLow, heightRulesHigh},
heightRulesLow = Map[Function[{vertex},
vertex -> Plus[1, Floor[Min[Catenate[Outer[
GraphDistance[g1, {#1, #2}, vertex] &,
MinMax[VertexList[g1]],
MinMax[VertexList[g1]]]]]/6]/2] ],
VertexList[g1]];
heightRulesHigh = MapThread[Rule, {Catenate[wallComponents],
Map[# + 1/2 &, Catenate[Table[First[First[
SortBy[Tally[DeleteCases[ReplaceAll[
Union[Catenate[Outer[Plus, #,
CirclePoints[{1, 0}, 4], 1]]],
heightRulesLow], _List]], Last]]],
Length[#]] & /@ wallComponents]]}];
{heightRulesLow, heightRulesHigh}
]
With[{heightRules = CompoundExpression[SeedRandom[21234312],
HeightRules[ResourceFunction["RandomSierpinskiMaze"][2][[1, 1]]]
]},
voxelSet = Graphics3D[Transpose[{{Lighter@Gray, Gray},
Map[Cuboid[# {1, 1, 0}, # + {1, 1, 0}] &,
MapApply[Append, #]] & /@ heightRules}],
ViewPoint -> {Infinity, -Infinity, Infinity},
ViewVertical -> {0, 0, 1},
Boxed -> False];
moveGraph = With[{g1 = NearestNeighborGraph[
MapApply[Append, Catenate[heightRules]],
{4, Sqrt[2]*.9}]}, Graph3D[g1,
VertexCoordinates -> Map[# -> (# + {1/2, 1/2, 1/4}) &,
VertexList[g1]],
VertexStyle -> Black, EdgeStyle -> Black]];
]
(This could really be any height map you want, even one ripped from a console game).
Finally, we introduce a few functions for moving pieces around, and plot the whole thing using a DynamicModule with EventHandler for key logging:
PlacePiece[primitives_][
index_, angle_, pos_, col_ : {Yellow, Orange}
] := Graphics3D[{EdgeForm[None],
Riffle[col,
Translate[Rotate[
#, angle, {0, 0, 1}, {1/2, 1/2, 0}
], pos] & /@ primitives[[index]]]}
]
MovePiece[moveGraph_][pos_, step_] := With[
{next = SelectFirst[
VertexOutComponent[moveGraph, pos, {1}],
#[[1 ;; 2]] == Plus[pos, step][[1 ;; 2]] &, True]},
If[TrueQ[next], pos, next]
]
DynamicModule[{
views = Catenate[Outer[
{#1 Infinity, #2 Infinity, Infinity} &,
{1, -1}, {1, -1}]][[{1, 2, 4, 3}]],
verticals = Catenate[Outer[
{If[#1 , #2, 0], If[#1 , 0, #2], 0} &,
{True, False}, {-1, 1}]][[{3, 1, 4, 2}]],
allpos = If[False, {
{3, 3, 1}, {4, 3, 1}, {5, 3, 1}, {6, 3, 1},
{3, 2, 1}, {4, 2, 1}, {5, 2, 1}, {6, 2, 1},
{29, 3, 1}, {29, 4, 1}, {29, 5, 1}, {29, 6, 1},
{30, 3, 1}, {30, 4, 1}, {30, 5, 1}, {30, 6, 1},
{3, 29, 1}, {4, 29, 1}, {5, 29, 1}, {6, 29, 1},
{3, 30, 1}, {4, 30, 1}, {5, 30, 1}, {6, 30, 1},
{29, 29, 1}, {28, 29, 1}, {27, 29, 1}, {26, 29, 1},
{29, 30, 1}, {28, 30, 1}, {27, 30, 1}, {26, 30, 1}
}, RandomSample[VertexList[moveGraph], 32]],
allface = Join[
ConstantArray[2, 8],
ConstantArray[1, 8],
ConstantArray[4, 16]
],
allind = {
1, 1, 1, 1, 2, 3, 4, 5,
1, 1, 1, 1, 6, 4, 3, 2,
1, 1, 1, 1, 2, 3, 4, 5,
1, 1, 1, 1, 2, 3, 4, 6
},
allcolor = Join[
ConstantArray[1, 16],
ConstantArray[2, 16]
],
who = 1,
top = False,
graph = False,
pos, face, obstructedMoveGraph,
dir = 0},
pos = allpos[[who]];
face = allface[[who]];
obstructedMoveGraph =
VertexDelete[moveGraph,
Alternatives @@ Complement[allpos, {allpos[[who]]}]];
EventHandler[Dynamic@Show[
voxelSet,
If[graph, obstructedMoveGraph, Graphics3D[{}]],
PlacePiece[primitives][allind[[who]], -(allface[[who]] + 1) *Pi/2,
allpos[[who]],
Association[{
1 -> {Red, Lighter[Orange, .5]},
2 -> Lighter@{Red, Lighter[Yellow, .5]}}][allcolor[[who]]]
],
MapThread[
PlacePiece[primitives][#1, -(#2 + 1) *Pi/2, #3, Association[{
1 -> {Yellow, Orange}, 2 -> {Orange, Yellow}}][#4]] &,
{allind, allface, allpos, allcolor}[[All,
Complement[Range[32], {who}]]]
],
ViewPoint -> If[top, {0, 0, Infinity}, views[[dir + 1]]],
ViewVertical -> If[top, verticals[[dir + 1]], {0, 0, 1}],
PlotRange -> {{0, 33}, {0, 33}, {0, 10}},
Boxed -> False,
ImageSize -> {1200, UpTo[800]}
], {
{"KeyDown", "w"} :> (dir = Mod[dir - 1, 4]),
{"KeyDown", "q"} :> (dir = Mod[dir + 1, 4]),
{"KeyDown", "t"} :> (top = Not[top]),
{"KeyDown", "g"} :> (graph = Not[graph]),
{"KeyDown", "c"} :> (who = Mod[who + 1, 32, 1];
obstructedMoveGraph =
VertexDelete[moveGraph,
Alternatives @@ Complement[allpos, {allpos[[who]]}]]),
{"KeyDown", "x"} :> (who = Mod[who - 1, 32, 1];
obstructedMoveGraph =
VertexDelete[moveGraph,
Alternatives @@ Complement[allpos, {allpos[[who]]}]]),
"UpArrowKeyDown" :> (allpos[[who]] =
MovePiece[obstructedMoveGraph][allpos[[who]],
verticals[[Mod[allface[[who]] = dir, 4] + 1]]]),
"RightArrowKeyDown" :> (allpos[[who]] =
MovePiece[obstructedMoveGraph][allpos[[who]],
verticals[[Mod[allface[[who]] = dir + 1, 4] + 1]]]),
"DownArrowKeyDown" :> (allpos[[who]] =
MovePiece[obstructedMoveGraph][allpos[[who]],
verticals[[Mod[allface[[who]] = dir + 2, 4] + 1]]]),
"LeftArrowKeyDown" :> (allpos[[who]] =
MovePiece[obstructedMoveGraph][allpos[[who]],
verticals[[Mod[allface[[who]] = dir + 3, 4] + 1]]])
}]]

The controls are as follows. Press "q" (or reverse "w") rotates camera:

Press "t" to toggle top down view:
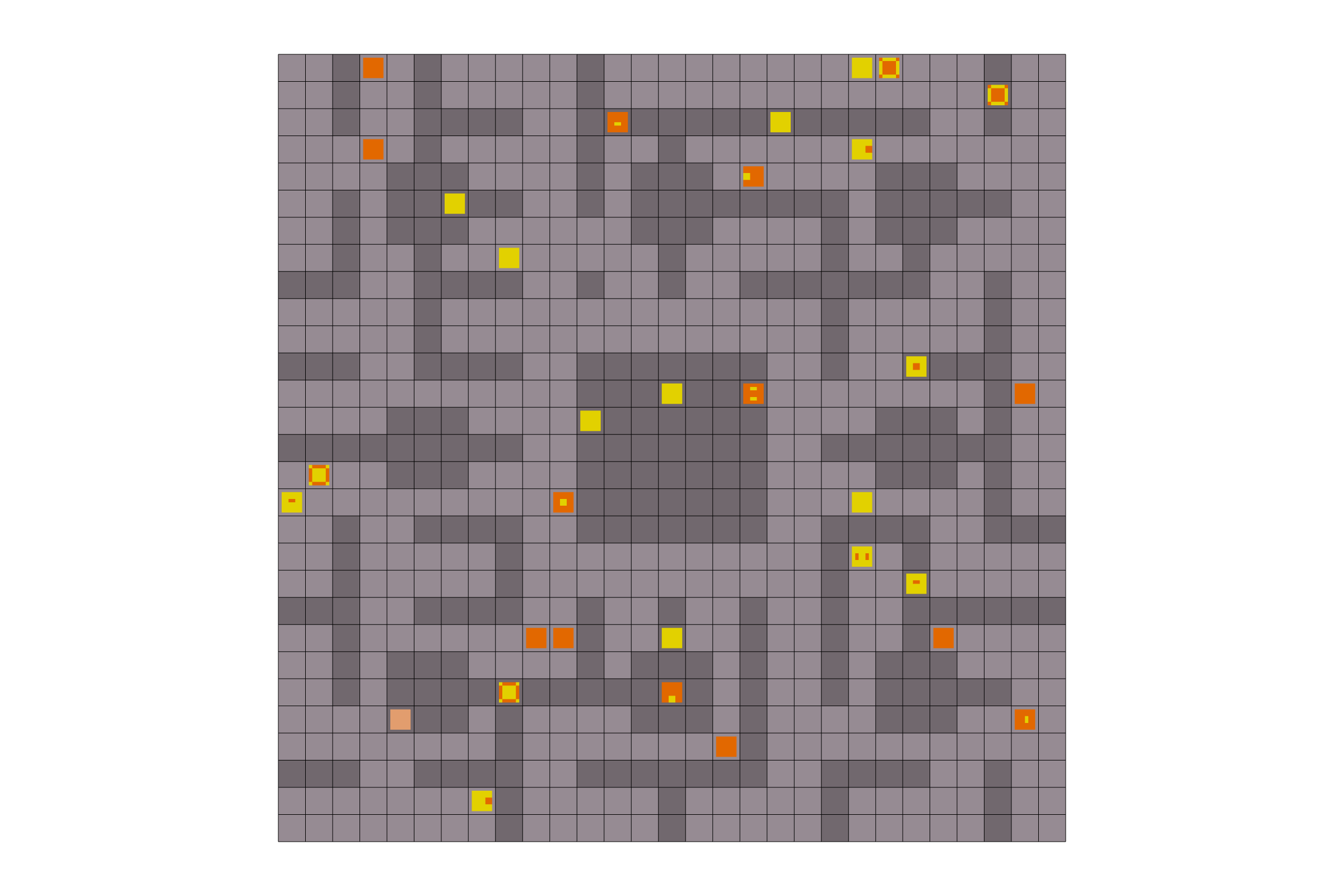
(notice pieces can be uniquely id'ed from top down view)
press "g" to toggle states adjacency graph:

press "t" to toggle back to isomorphic view:

Arrow keys move the current selected piece, shown in lighter colors with red accents, and "c" and "x" cycle the piece selector through 32 alternatives. Here's a good initial condition:

Of course, this needs more automation, more flexible movement rules, menus, etc. etc. but I think it's already somewhat playable as is.